Considere una fila de n monedas de valores v1. . . vn, donde n es par. Jugamos un juego contra un oponente alternando turnos. En cada turno, un jugador selecciona la primera o la última moneda de la fila, la retira de la fila de forma permanente y recibe el valor de la moneda. Determine la máxima cantidad posible de dinero que definitivamente podemos ganar si nos movemos primero.
Además, imprima la secuencia de movimientos en el juego óptimo. Como muchas secuencias de movimientos pueden conducir a la respuesta óptima, puede imprimir cualquier secuencia válida.
Antes de la secuencia, la parte ya se comenta en estos artículos.
Ejemplos:
Entrada: 10 80 90 30
Salida: 110 RRRL
Explicación:
P1 elige 30, P2 elige 90, P1 elige 80 y finalmente P2 elige 10. La
puntuación obtenida por P1 es 80 + 30 = 110 La
puntuación máxima posible para el jugador 1 es: 110
Juego óptimo los movimientos son: RRRLEntrada: 10 100 10
Salida: 20 RRL
Aproximación:
en cada turno (excepto el último), un jugador tendrá dos opciones: recoger la bolsa de la izquierda o recoger la bolsa de la derecha de la fila. Nuestro objetivo es evaluar la puntuación máxima que puede obtener P1, sea S. A P1 le gustaría elegir la puntuación máxima posible en su turno, mientras que a P2 le gustaría elegir la puntuación mínima posible para P1.
Entonces P1 se enfoca en maximizar S, mientras que P2 se enfoca en minimizar S.
Enfoque ingenuo:
- Podemos escribir una solución recursiva de fuerza bruta al problema que simule todas las posibilidades del juego y encuentre la puntuación máxima bajo las restricciones dadas.
- La función maxScore devuelve la puntuación máxima posible para el jugador 1 y también los movimientos que tienen lugar a lo largo del juego.
- Dado que la función necesita devolver tanto el puntaje máximo posible como los movimientos que conducen a ese puntaje, usamos un par de entero y string.
- La string que representa los movimientos del juego consta de caracteres ‘L’ y ‘R’, lo que significa que se eligió la bolsa más a la izquierda o más a la derecha, respectivamente.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation
#include <bits/stdc++.h>
using namespace std;
// Calculates the maximum score
// possible for P1 If only the
// bags from beg to ed were available
pair<int, string> maxScore(vector<int> money,
int beg,
int ed)
{
// Length of the game
int totalTurns = money.size();
// Which turn is being played
int turnsTillNow = beg
+ ((totalTurns - 1) - ed);
// Base case i.e last turn
if (beg == ed) {
// if it is P1's turn
if (turnsTillNow % 2 == 0)
return { money[beg], "L" };
// if P2's turn
else
return { 0, "L" };
}
// Player picks money from
// the left end
pair<int, string> scoreOne
= maxScore(money,
beg + 1,
ed);
// Player picks money from
// the right end
pair<int, string> scoreTwo
= maxScore(money, beg, ed - 1);
if (turnsTillNow % 2 == 0) {
// if it is player 1's turn then
// current picked score added to
// his total. choose maximum of
// the two scores as P1 tries to
// maximize his score.
if (money[beg] + scoreOne.first
> money[ed] + scoreTwo.first) {
return { money[beg] + scoreOne.first,
"L" + scoreOne.second };
}
else
return { money[ed] + scoreTwo.first,
"R" + scoreTwo.second };
}
// if player 2's turn don't add
// current picked bag score to
// total. choose minimum of the
// two scores as P2 tries to
// minimize P1's score.
else {
if (scoreOne.first < scoreTwo.first)
return { scoreOne.first,
"L" + scoreOne.second };
else
return { scoreTwo.first,
"R" + scoreTwo.second };
}
}
// Driver Code
int main()
{
// Input array
int ar[] = { 10, 80, 90, 30 };
int arraySize = sizeof(ar) / sizeof(int);
vector<int> bags(ar, ar + arraySize);
// Function Calling
pair<int, string> ans
= maxScore(bags,
0,
bags.size() - 1);
cout << ans.first << " " << ans.second << endl;
return 0;
}
Python3
# Python3 implementation # Calculates the maximum score # possible for P1 If only the # bags from beg to ed were available def maxScore( money, beg, ed): # Length of the game totalTurns = len(money) # Which turn is being played turnsTillNow = beg + ((totalTurns - 1) - ed) # Base case i.e last turn if (beg == ed): # if it is P1's turn if (turnsTillNow % 2 == 0): return [money[beg], "L"] # if P2's turn else: return [0, "L"] # Player picks money from # the left end scoreOne = maxScore(money, beg + 1, ed) # Player picks money from # the right end scoreTwo = maxScore(money, beg, ed - 1) if (turnsTillNow % 2 == 0): # If it is player 1's turn then # current picked score added to # his total. choose maximum of # the two scores as P1 tries to # maximize his score. if (money[beg] + scoreOne[0] > money[ed] + scoreTwo[0]): return [money[beg] + scoreOne[0], "L" + scoreOne[1]] else: return [money[ed] + scoreTwo[0], "R" + scoreTwo[1]] # If player 2's turn don't add # current picked bag score to # total. choose minimum of the # two scores as P2 tries to # minimize P1's score. else: if (scoreOne[0] < scoreTwo[0]): return[scoreOne[0], "L" + scoreOne[1]] else: return[scoreTwo[0], "R" + scoreTwo[1]] # Driver Code # Input array ar = [ 10, 80, 90, 30 ] arraySize = len(ar) bags = ar # Function Calling ans = maxScore(bags, 0, arraySize - 1) print(ans[0], ans[1]) # This code is contributed by shivani
C#
// C# implementation
using System;
using System.Collections.Generic;
class GFG {
// Calculates the maximum score
// possible for P1 If only the
// bags from beg to ed were available
static Tuple<int,string> maxScore(List<int> money, int beg, int ed)
{
// Length of the game
int totalTurns = money.Count;
// Which turn is being played
int turnsTillNow = beg + ((totalTurns - 1) - ed);
// Base case i.e last turn
if (beg == ed)
{
// if it is P1's turn
if (turnsTillNow % 2 == 0)
return new Tuple<int,string>(money[beg], "L");
// if P2's turn
else
return new Tuple<int,string>(0, "L");
}
// Player picks money from
// the left end
Tuple<int,string> scoreOne = maxScore(money, beg + 1, ed);
// Player picks money from
// the right end
Tuple<int,string> scoreTwo = maxScore(money, beg, ed - 1);
if (turnsTillNow % 2 == 0)
{
// if it is player 1's turn then
// current picked score added to
// his total. choose maximum of
// the two scores as P1 tries to
// maximize his score.
if (money[beg] + scoreOne.Item1
> money[ed] + scoreTwo.Item1)
{
return new Tuple<int,string>(money[beg] + scoreOne.Item1, "L" + scoreOne.Item2);
}
else
return new Tuple<int,string>(money[ed] + scoreTwo.Item1, "R" + scoreTwo.Item2);
}
// if player 2's turn don't add
// current picked bag score to
// total. choose minimum of the
// two scores as P2 tries to
// minimize P1's score.
else {
if (scoreOne.Item1 < scoreTwo.Item1)
return new Tuple<int,string>(scoreOne.Item1, "L" + scoreOne.Item2);
else
return new Tuple<int,string>(scoreTwo.Item1+110, "R" + scoreTwo.Item2);
}
}
static void Main() {
// Input array
int[] ar = { 10, 80, 90, 30 };
int arraySize = ar.Length;
List<int> bags = new List<int>(new int[arraySize]);
// Function Calling
Tuple<int, string> ans = maxScore(bags, 0, bags.Count - 1);
Console.Write(ans.Item1 + " " + ans.Item2);
}
}
// This code is contributed by suresh07.
Javascript
<script>
// Javascript implementation
// Calculates the maximum score
// possible for P1 If only the
// bags from beg to ed were available
function maxScore(money, beg, ed)
{
// Length of the game
let totalTurns = money.length;
// Which turn is being played
let turnsTillNow = beg + ((totalTurns - 1) - ed);
// Base case i.e last turn
if (beg == ed)
{
// if it is P1's turn
if (turnsTillNow % 2 == 0)
return [money[beg], "L"];
// if P2's turn
else
return [0, "L"];
}
// Player picks money from
// the left end
let scoreOne = maxScore(money, beg + 1, ed);
// Player picks money from
// the right end
let scoreTwo = maxScore(money, beg, ed - 1);
if (turnsTillNow % 2 == 0)
{
// if it is player 1's turn then
// current picked score added to
// his total. choose maximum of
// the two scores as P1 tries to
// maximize his score.
if (money[beg] + scoreOne[0]
> money[ed] + scoreTwo[0])
{
return [money[beg] + scoreOne[0], "L" + scoreOne[1]];
}
else
return [money[ed] + scoreTwo[[0]], "R" + scoreTwo[1]];
}
// if player 2's turn don't add
// current picked bag score to
// total. choose minimum of the
// two scores as P2 tries to
// minimize P1's score.
else {
if (scoreOne.first < scoreTwo.first)
return [scoreOne[0], "L" + scoreOne[1]];
else
return [scoreTwo[0], "R" + scoreTwo[1]];
}
}
// Driver Code
// Input array
let ar = [10, 80, 90, 30];
let arraySize = ar.length;
let bags = ar;
// Function Calling
let ans = maxScore(bags, 0, bags.length - 1);
document.write(ans[0] + " " + ans[1] + "<br>");
// This code is contributed by gfgking.
</script>
Producción:
110 RRRL
La complejidad temporal del enfoque anterior es exponencial.
Enfoque óptimo:
podemos resolver este problema mediante el uso de programación dinámica en 
la complejidad del tiempo y el espacio.
- Si almacenamos las mejores respuestas posibles para todas las bolsas desde algún principio i hasta algún final j , entonces puede haber a lo sumo
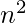subproblemas diferentes. - Sea dp(i, j) la puntuación máxima que P1 puede alcanzar si las únicas bolsas que quedan en la fila comienzan en i y terminan en j . Entonces se mantiene lo siguiente:
- si es el turno de P1
- dp(i, j) = puntuación máxima de la bolsa i + dp(i+1, j) o puntuación de la bolsa j + dp(i, j-1) .
- si es el turno de P2
- dp(i, j) = mínimo de dp(i+1, j) o dp(i, j-1) .
Dado que el puntaje de la bolsa actual va a P2, no lo agregamos a dp(i, j) .
- dp(i, j) = mínimo de dp(i+1, j) o dp(i, j-1) .
- si es el turno de P1
- Para realizar un seguimiento de los movimientos que tienen lugar en un estado dado, mantenemos una array booleana adicional que nos permite reconstruir los movimientos completos del juego que conducen a la puntuación máxima.
- La array leftBag(i, j) representa un estado en el que solo están presentes las bolsas de i a j . leftBag(i, j) es 1 si es óptimo elegir el leftBag; de lo contrario, es 0 .
- La función getMoves usa esta array para reconstruir los movimientos correctos.
A continuación se muestra la implementación del enfoque anterior:
C++
// C++ implementation
#include <bits/stdc++.h>
#define maxSize 3000
using namespace std;
// dp(i, j) is the best
// score possible if only
// the bags from i, j were
// present.
int dp[maxSize][maxSize];
// leftBag(i, j) is 1 if in the
// optimal game the player picks
// the leftmost bag when only the
// bags from i to j are present.
bool leftBag[maxSize][maxSize];
// Function to calculate the maximum
// value
int maxScore(vector<int> money)
{
// we will fill the dp table
// in a bottom-up manner. fill
// all states that represent
// lesser number of bags before
// filling states that represent
// higher number of bags.
// we start from states dp(i, i)
// as these are the base case of
// our DP solution.
int n = money.size();
int totalTurns = n;
// turn = 1 if it is player 1's
// turn else 0. Who gets to pick
// the last bag(bottom-up so we
// start from last turn)
bool turn
= (totalTurns % 2 == 0) ? 0 : 1;
// if bag is picked by P1 add it
// to the ans else 0 contribution
// to score.
for (int i = 0; i < n; i++) {
dp[i][i] = turn ? money[i] : 0;
leftBag[i][i] = 1;
}
// 2nd last bag is picked by
// the other player.
turn = !turn;
// sz represents the size
// or number of bags in
// the state dp(i, i+sz)
int sz = 1;
while (sz < n) {
for (int i = 0; i + sz < n; i++) {
int scoreOne = dp[i + 1][i + sz];
int scoreTwo = dp[i][i + sz - 1];
// First player
if (turn) {
dp[i][i + sz]
= max(money[i] + scoreOne,
money[i + sz] + scoreTwo);
// if leftBag has more profit
if (money[i] + scoreOne
> money[i + sz] + scoreTwo)
leftBag[i][i + sz] = 1;
else
leftBag[i][i + sz] = 0;
}
// second player
else {
dp[i][i + sz]
= min(scoreOne,
scoreTwo);
if (scoreOne < scoreTwo)
leftBag[i][i + sz] = 1;
else
leftBag[i][i + sz] = 0;
}
}
// Give turn to the
// other player.
turn = !turn;
// Now fill states
// with more bags.
sz++;
}
return dp[0][n - 1];
}
// Using the leftBag matrix,
// generate the actual game
// moves that lead to the score.
string getMoves(int n)
{
string moves;
int left = 0, right = n - 1;
while (left <= right) {
// if the bag is picked from left
if (leftBag[left][right]) {
moves.push_back('L');
left++;
}
else {
moves.push_back('R');
right--;
}
}
return moves;
}
// Driver Code
int main()
{
int ar[] = { 10, 80, 90, 30 };
int arraySize = sizeof(ar) / sizeof(int);
vector<int> bags(ar, ar + arraySize);
int ans = maxScore(bags);
cout << ans << " " << getMoves(bags.size());
return 0;
}
Java
// Java Implementation
public class Main
{
static int maxSize = 3000;
// dp(i, j) is the best
// score possible if only
// the bags from i, j were
// present.
static int[][] dp = new int[maxSize][maxSize];
// leftBag(i, j) is 1 if in the
// optimal game the player picks
// the leftmost bag when only the
// bags from i to j are present.
static boolean[][] leftBag = new boolean[maxSize][maxSize];
// Function to calculate the maximum
// value
static int maxScore(int[] money)
{
// we will fill the dp table
// in a bottom-up manner. fill
// all states that represent
// lesser number of bags before
// filling states that represent
// higher number of bags.
// we start from states dp(i, i)
// as these are the base case of
// our DP solution.
int n = money.length;
int totalTurns = n;
// turn = 1 if it is player 1's
// turn else 0. Who gets to pick
// the last bag(bottom-up so we
// start from last turn)
boolean turn = (totalTurns % 2 == 0) ? false : true;
// if bag is picked by P1 add it
// to the ans else 0 contribution
// to score.
for (int i = 0; i < n; i++) {
dp[i][i] = turn ? money[i] : 0;
leftBag[i][i] = true;
}
// 2nd last bag is picked by
// the other player.
turn = !turn;
// sz represents the size
// or number of bags in
// the state dp(i, i+sz)
int sz = 1;
while (sz < n) {
for (int i = 0; i + sz < n; i++) {
int scoreOne = dp[i + 1][i + sz];
int scoreTwo = dp[i][i + sz - 1];
// First player
if (turn) {
dp[i][i + sz] = Math.max(money[i] + scoreOne, money[i + sz] + scoreTwo);
// if leftBag has more profit
if (money[i] + scoreOne > money[i + sz] + scoreTwo)
leftBag[i][i + sz] = true;
else
leftBag[i][i + sz] = false;
}
// second player
else {
dp[i][i + sz] = Math.min(scoreOne, scoreTwo);
if (scoreOne < scoreTwo)
leftBag[i][i + sz] = true;
else
leftBag[i][i + sz] = false;
}
}
// Give turn to the
// other player.
turn = !turn;
// Now fill states
// with more bags.
sz++;
}
return dp[0][n - 1];
}
// Using the leftBag matrix,
// generate the actual game
// moves that lead to the score.
static String getMoves(int n)
{
String moves = "";
int left = 0, right = n - 1;
while (left <= right) {
// if the bag is picked from left
if (leftBag[left][right]) {
moves = moves + 'L';
left++;
}
else {
moves = moves + 'R';
right--;
}
}
return moves;
}
public static void main(String[] args) {
for(int i = 0; i < maxSize; i++)
{
for(int j = 0; j < maxSize; j++)
{
dp[i][j] = 0;
leftBag[i][j] = false;
}
}
int[] ar = { 10, 80, 90, 30 };
int arraySize = ar.length;
int[] bags = ar;
int ans = maxScore(bags);
System.out.print(ans + " " + getMoves(bags.length));
}
}
// This code is contributed by divyes072019.
Python3
# Python3 Implementation maxSize = 3000 # dp(i, j) is the best # score possible if only # the bags from i, j were # present. dp = [[0 for i in range(maxSize)] for j in range(maxSize)] # leftBag(i, j) is 1 if in the # optimal game the player picks # the leftmost bag when only the # bags from i to j are present. leftBag = [[False for i in range(maxSize)] for j in range(maxSize)] # Function to calculate the maximum # value def maxScore(money): # we will fill the dp table # in a bottom-up manner. fill # all states that represent # lesser number of bags before # filling states that represent # higher number of bags. # we start from states dp(i, i) # as these are the base case of # our DP solution. n = len(money) totalTurns = n # turn = 1 if it is player 1's # turn else 0. Who gets to pick # the last bag(bottom-up so we # start from last turn) turn = 0 if (totalTurns % 2 == 0) else 1 # if bag is picked by P1 add it # to the ans else 0 contribution # to score. for i in range(n): dp[i][i] = money[i] if turn else 0 leftBag[i][i] = 1 # 2nd last bag is picked by # the other player. turn = not turn # sz represents the size # or number of bags in # the state dp(i, i+sz) sz = 1 while sz < n: i = 0 while i + sz < n: scoreOne = dp[i + 1][i + sz] scoreTwo = dp[i][i + sz - 1] # First player if turn: dp[i][i + sz] = max(money[i] + scoreOne, money[i + sz] + scoreTwo) # if leftBag has more profit if (money[i] + scoreOne > money[i + sz] + scoreTwo): leftBag[i][i + sz] = 1 else: leftBag[i][i + sz] = 0 # second player else: dp[i][i + sz] = min(scoreOne, scoreTwo) if (scoreOne < scoreTwo): leftBag[i][i + sz] = 1 else: leftBag[i][i + sz] = 0 i += 1 # Give turn to the # other player. turn = not turn # Now fill states # with more bags. sz += 1 return dp[0][n - 1] # Using the leftBag matrix, # generate the actual game # moves that lead to the score. def getMoves(n): moves = "" left, right = 0, n - 1 while (left <= right): # if the bag is picked from left if (leftBag[left][right]): moves = moves + 'L' left += 1 else: moves = moves + 'R' right -= 1 return moves ar = [ 10, 80, 90, 30 ] arraySize = len(ar) bags = ar ans = maxScore(bags) print(ans, getMoves(len(bags)), sep=" ") # This code is contributed by mukesh07.
C#
// C# Implementation
using System;
class GFG {
static int maxSize = 3000;
// dp(i, j) is the best
// score possible if only
// the bags from i, j were
// present.
static int[,] dp = new int[maxSize, maxSize];
// leftBag(i, j) is 1 if in the
// optimal game the player picks
// the leftmost bag when only the
// bags from i to j are present.
static bool[,] leftBag = new bool[maxSize, maxSize];
// Function to calculate the maximum
// value
static int maxScore(int[] money)
{
// we will fill the dp table
// in a bottom-up manner. fill
// all states that represent
// lesser number of bags before
// filling states that represent
// higher number of bags.
// we start from states dp(i, i)
// as these are the base case of
// our DP solution.
int n = money.Length;
int totalTurns = n;
// turn = 1 if it is player 1's
// turn else 0. Who gets to pick
// the last bag(bottom-up so we
// start from last turn)
bool turn = (totalTurns % 2 == 0) ? false : true;
// if bag is picked by P1 add it
// to the ans else 0 contribution
// to score.
for (int i = 0; i < n; i++) {
dp[i,i] = turn ? money[i] : 0;
leftBag[i,i] = true;
}
// 2nd last bag is picked by
// the other player.
turn = !turn;
// sz represents the size
// or number of bags in
// the state dp(i, i+sz)
int sz = 1;
while (sz < n) {
for (int i = 0; i + sz < n; i++) {
int scoreOne = dp[i + 1,i + sz];
int scoreTwo = dp[i,i + sz - 1];
// First player
if (turn) {
dp[i,i + sz] = Math.Max(money[i] + scoreOne, money[i + sz] + scoreTwo);
// if leftBag has more profit
if (money[i] + scoreOne > money[i + sz] + scoreTwo)
leftBag[i,i + sz] = true;
else
leftBag[i,i + sz] = false;
}
// second player
else {
dp[i,i + sz] = Math.Min(scoreOne, scoreTwo);
if (scoreOne < scoreTwo)
leftBag[i, i + sz] = true;
else
leftBag[i, i + sz] = false;
}
}
// Give turn to the
// other player.
turn = !turn;
// Now fill states
// with more bags.
sz++;
}
return dp[0,n - 1];
}
// Using the leftBag matrix,
// generate the actual game
// moves that lead to the score.
static string getMoves(int n)
{
string moves = "";
int left = 0, right = n - 1;
while (left <= right) {
// if the bag is picked from left
if (leftBag[left,right]) {
moves = moves + 'L';
left++;
}
else {
moves = moves + 'R';
right--;
}
}
return moves;
}
static void Main()
{
for(int i = 0; i < maxSize; i++)
{
for(int j = 0; j < maxSize; j++)
{
dp[i,j] = 0;
leftBag[i,j] = false;
}
}
int[] ar = { 10, 80, 90, 30 };
int arraySize = ar.Length;
int[] bags = ar;
int ans = maxScore(bags);
Console.Write(ans + " " + getMoves(bags.Length));
}
}
// This code is contributed by decode2207.
Javascript
<script>
// Javascript Implementation
let maxSize = 3000;
// dp(i, j) is the best
// score possible if only
// the bags from i, j were
// present.
let dp = new Array(maxSize);
for(let i = 0; i < maxSize; i++)
{
dp[i] = new Array(maxSize);
for(let j = 0; j < maxSize; j++)
{
dp[i][j] = 0;
}
}
// leftBag(i, j) is 1 if in the
// optimal game the player picks
// the leftmost bag when only the
// bags from i to j are present.
let leftBag = new Array(maxSize);
for(let i = 0; i < maxSize; i++)
{
leftBag[i] = new Array(maxSize);
for(let j = 0; j < maxSize; j++)
{
leftBag[i][j] = false;
}
}
// Function to calculate the maximum
// value
function maxScore(money)
{
// we will fill the dp table
// in a bottom-up manner. fill
// all states that represent
// lesser number of bags before
// filling states that represent
// higher number of bags.
// we start from states dp(i, i)
// as these are the base case of
// our DP solution.
let n = money.length;
let totalTurns = n;
// turn = 1 if it is player 1's
// turn else 0. Who gets to pick
// the last bag(bottom-up so we
// start from last turn)
let turn = (totalTurns % 2 == 0) ? 0 : 1;
// if bag is picked by P1 add it
// to the ans else 0 contribution
// to score.
for (let i = 0; i < n; i++) {
dp[i][i] = turn ? money[i] : 0;
leftBag[i][i] = 1;
}
// 2nd last bag is picked by
// the other player.
turn = !turn;
// sz represents the size
// or number of bags in
// the state dp(i, i+sz)
let sz = 1;
while (sz < n) {
for (let i = 0; i + sz < n; i++) {
let scoreOne = dp[i + 1][i + sz];
let scoreTwo = dp[i][i + sz - 1];
// First player
if (turn) {
dp[i][i + sz]
= Math.max(money[i] + scoreOne,
money[i + sz] + scoreTwo);
// if leftBag has more profit
if (money[i] + scoreOne
> money[i + sz] + scoreTwo)
leftBag[i][i + sz] = 1;
else
leftBag[i][i + sz] = 0;
}
// second player
else {
dp[i][i + sz]
= Math.min(scoreOne,
scoreTwo);
if (scoreOne < scoreTwo)
leftBag[i][i + sz] = 1;
else
leftBag[i][i + sz] = 0;
}
}
// Give turn to the
// other player.
turn = !turn;
// Now fill states
// with more bags.
sz++;
}
return dp[0][n - 1];
}
// Using the leftBag matrix,
// generate the actual game
// moves that lead to the score.
function getMoves(n)
{
let moves = "";
let left = 0, right = n - 1;
while (left <= right) {
// if the bag is picked from left
if (leftBag[left][right]) {
moves = moves + 'L';
left++;
}
else {
moves = moves + 'R';
right--;
}
}
return moves;
}
let ar = [ 10, 80, 90, 30 ];
let arraySize = ar.length;
let bags = ar;
let ans = maxScore(bags);
document.write(ans + " " + getMoves(bags.length));
// This code is contributed by divyeshrabadiya07.
</script>
Producción:
110 RRRL
Las complejidades de tiempo y espacio de este enfoque son 
.
Publicación traducida automáticamente
Artículo escrito por KartikArora y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA