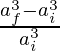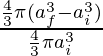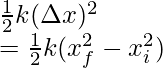Tensión, deformación y energía potencial elástica

Elasticidad, este término siempre recuerda a objetos como gomas elásticas, etc. Sin embargo, si surge la pregunta, ¿cuál es más elástica, una goma o una pieza de hierro? La respuesta será una pieza de hierro. ¿Por qué? La respuesta se encuentra en la definición de elasticidad, se sabe que la elasticidad es la capacidad del objeto para restaurar su forma original después de que se aplica la fuerza al objeto que deforma su forma. Aprendamos sobre la elasticidad con más detalle,

Estrés y tensión

Cuando se aplican fuerzas a cuerpos de naturaleza elástica, se produce en ellos una deformación temporal que depende de la naturaleza del material. Esta deformación no suele ser visible, pero produce una fuerza restauradora que tiende a devolver el cuerpo a su estado natural. La magnitud de la fuerza restauradora es igual a la fuerza que se aplica al cuerpo. El estrés se ha definido como la fuerza restauradora por unidad de área.

Sea F la magnitud de la fuerza aplicada sobre el cuerpo y A el área,

Estrés = $\frac{F}{A}$

El estrés se puede clasificar en tres categorías. Considere un ejemplo para comprender cómo actúan las fuerzas sobre estas tensiones:

Tensión de tracción/compresión : en este tipo de tensión, la fuerza es perpendicular a la sección transversal del cilindro.
Esfuerzo cortante : La fuerza se aplica paralelamente al área de la sección transversal del cilindro.
Estrés Hidráulico: La fuerza se aplica a todo el cuerpo

La deformación es la relación entre el cambio de dimensión y la dimensión original. Por ejemplo, en el caso anterior de un cilindro, diferentes tipos de esfuerzos provocan diferentes cambios en las dimensiones del cilindro. En el caso de esfuerzo de compresión o tracción, se cambia la longitud del cilindro.

Sea $\Delta L$ L el cambio de longitud del cilindro y L la longitud original. Esto se llama deformación longitudinal. está dado por,

$\text{Longitudinal Strain }= \frac{\Delta L}{L}$

En el caso de esfuerzo cortante,

$\text{Shearing Strain }= \frac{x}{L} = tan(\theta)$

Aquí, $\theta$ es el desplazamiento angular del cilindro desde su posición media.

Cuando se aplica tensión hidráulica, el cuerpo cambia su volumen. En este caso, se utiliza la deformación volumétrica.

$\text{Volumetric Strain }= \frac{\Delta V}{V}$

Ley de Hooke

La ley de Hooke se basa en evidencia empírica y es válida para casi todos los materiales. Ayuda a establecer una relación entre la tensión y la deformación en forma de una curva de tensión-deformación. Estas curvas varían de material a material y son muy útiles para dar una idea clara de cómo se comporta el material en diferentes condiciones de carga. Sin embargo, esta ley solo es aplicable para pequeños desplazamientos. De acuerdo con la ley de Hooke, para pequeñas deformaciones, el esfuerzo y la deformación que se producen en el cuerpo son directamente proporcionales entre sí.

Estrés ∝ Deformación

⇒ Tensión = kx Deformación

Aquí, k es la constante de proporcionalidad y se denomina módulo de elasticidad.

Energía potencial elástica

La energía potencial elástica es la energía almacenada en un objeto debido a su deformación. Cuando se aplica una fuerza a un objeto para deformar su forma y tamaño, funciona contra una fuerza restauradora. De esta manera, el trabajo realizado sobre el objeto se almacena en forma de energía potencial del objeto. Esta energía se llama energía potencial elástica. Muchas veces, los objetos están diseñados específicamente para almacenar la energía potencial elástica.

Una primavera ideal
Pelota saltarina que se comprime al tocar el suelo.
El arco estirado de un arquero.

Energía potencial elástica almacenada en el resorte.

Cuando un resorte se comprime con una fuerza F produciendo el cambio de longitud $\Delta x$ . Comienza a actuar una fuerza restauradora que trata de devolver el cuerpo a una posición de equilibrio. Esta fuerza sigue la ley de Hooke. El trabajo realizado por esta fuerza para el cambio de longitud $\Delta x$ se puede calcular mediante los métodos de integración o por el área bajo la curva de la ley de Hooke.

Energía potencial elástica almacenada en el resorte = Trabajo realizado por la fuerza

= $\frac{1}{2}k(\Delta x)^2$

Energía potencial elástica almacenada en otros materiales plásticos

Spring es un ejemplo de un objeto diseñado para aprovechar las propiedades elásticas del material. En el caso general de cualquier material, la energía almacenada por compresión o elongación se calcula a través de la curva tensión-deformación. El área bajo esta curva nos da la energía potencial elástica almacenada en el material debido al trabajo realizado por la fuerza de restauración.

En el caso de materiales tridimensionales que obedecen la Ley de Hooke,

Energía potencial elástica = $\frac{1}{2}.\text{ Stress}.\text{ Strain}$

Problemas de muestra

Pregunta 1: Un cubo de 2 m de lado se encoge hasta una longitud de 0,5 m cuando se aplica tensión hidráulica. Encuentre la deformación volumétrica.

Responder:

La deformación volumétrica está dada por,

$\text{Volumetric Strain }= \frac{\Delta V}{V}$

El volumen de un cubo viene dado por A

V = un ³

Radio inicial: a _i = 2 m

Radio final: _af = 0,5m

Cambio en volumen = $a_f^3 - a_i^3$

= $2^3 - (0.5)^3$

= 7.875

Volumen original = a ³

= 1

Deformación volumétrica = $\frac{\text{Change in Volume}}{\text{Original Volume}}$

= $\frac{a_f^3 - a_i^3}{a_i^3}$

= $\frac{7.875}{1}$

=7.875

Pregunta 2: Una esfera de 2 m de radio se encoge hasta un radio de 1 m cuando se aplica tensión hidráulica. Encuentre la deformación volumétrica.

Responder:

La deformación volumétrica está dada por,

$\text{Volumetric Strain }= \frac{\Delta V}{V}$

El volumen de una esfera está dado por A

V = $\frac{4}{3}\pi r^3$

Radio inicial: r _i = 2 m

Radio final: r _f = 1 m

Cambio en volumen = $\frac{4}{3}\pi (a_f^3 - a_i^3)$

= $\frac{4}{3} \pi (2^3 - 1^3)$

= $\frac{4}{3} \pi.7$

Volumen original = $\frac{4}{3} \pi r_f^3$

= $\frac{4}{3} \pi$

Deformación volumétrica = $\frac{\text{Change in Volume}}{\text{Original Volume}}$

= $\frac{\frac{4}{3}\pi (a_f^3 - a_i^3)}{\frac{4}{3} \pi a_i^3}$

= $\frac{7}{1}$

=7

Pregunta 3: Un cubo de 1,5 m de lado se encoge hasta una longitud de 0,5 m cuando se aplica una fuerza de compresión de 100 N. Encuentre el esfuerzo de compresión.

Responder:

El esfuerzo de compresión está dado por,

Estrés = $\frac{F}{A}$

En este caso, F = 100N y A = lado ^2.

El lado se da como 1,5 m.

A = lado ^2.

⇒A = 1.5 ²

⇒ A = 2,25

Estrés = $\frac{F}{A}$

⇒ Estrés = $\frac{100}{2.25}$

⇒ Tensión = 44,44 N/m ²

Pregunta 4: Un cubo de 3 m de lado se encoge hasta una longitud de 1 m cuando se aplica una fuerza de compresión de 500 N. Encuentre el esfuerzo de compresión.

Responder:

El esfuerzo de compresión está dado por,

Estrés = $\frac{F}{A}$

En este caso, F = 500N y A = lado ^2.

El lado se da como 32m

A = lado ^2.

⇒A = 3 ²

⇒ A = 9

Estrés = $\frac{F}{A}$

⇒ Estrés = $\frac{500}{9}$

⇒ Tensión =55,5 N/m ²

Pregunta 5: Un resorte con k = 50 N/m se comprime desde su longitud natural de 1 ma 0,5 m. Encuentre la energía potencial elástica almacenada en el resorte.

Responder:

La energía almacenada en el resorte está dada por,

EPE = $\frac{1}{2}k(\Delta x)^2$

Aquí, k = 50 N/m y $\Delta x = 0.5$

Reemplazando los valores en la ecuación dada,

EPE = $\frac{1}{2}k(\Delta x)^2$

⇒ EEP = $\frac{1}{2}(50)(0.5)^2$

⇒ EPE = (25)(0.25)

⇒EPE = 6.25J

Pregunta 6: Un resorte con k = 100 N/m se comprime desde su longitud natural de 2 ma 1 m. Encuentre la energía potencial elástica almacenada en el resorte.

Responder:

La energía almacenada en el resorte está dada por,

EPE = $\frac{1}{2}k(\Delta x)^2$

Aquí, k = 100 N/m y $\Delta x = 1$

Reemplazando los valores en la ecuación dada,

EPE = $\frac{1}{2}k(\Delta x)^2$

⇒ EEP = $\frac{1}{2}(100)(1)^2$

⇒EPE = 50J

Pregunta 7: Un resorte con k = 50 N/m se comprime desde su longitud natural de 1 ma 0,5 m. Encuentre la energía potencial elástica almacenada en el resorte.

Responder:

La energía almacenada en el resorte está dada por,

EPE = $\frac{1}{2}k(\Delta x)^2$

Aquí, k = 50 N/m y $\Delta x = 0.5$

Reemplazando los valores en la ecuación dada,

EPE = $\frac{1}{2}k(\Delta x)^2$

⇒ EEP = $\frac{1}{2}(50)(0.5)^2$

⇒ EPE = (25)(0.25)

⇒EPE = 6.25J

Pregunta 8: Un resorte con k = 100 N/m se comprime desde su longitud natural a 0,5 m. Si la energía potencial elástica almacenada en el resorte es de 10J, encuentre la longitud natural del resorte.

Responder:

La energía almacenada en el resorte está dada por,

EPE = $\frac{1}{2}k(\Delta x)^2 \\ = \frac{1}{2}k(x_f^2 - x_i^2)$

Aquí, k = 50 N/m, x _f = 0,5 m y x _i = ?.

Reemplazando los valores en la ecuación dada,

EPE = $\frac{1}{2}k(x_f^2 - x_i^2)$

⇒ 10 = $\frac{1}{2}100(0.5^2 - x_i^2)$

⇒ 20 = 100(0.5 ² – x _i² )

⇒ 0,2 = 0,25 – x _yo²

⇒x _i² = 0.25 – 0.2

⇒x _i² = 0.05

⇒x _yo = √0.05

⇒x _yo = 0.223

Publicación traducida automáticamente

Artículo escrito por anjalishukla1859 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Estrés y tensión

Ley de Hooke

Energía potencial elástica

Problemas de muestra

Deja una respuesta Cancelar la respuesta