Tango Tree es un algoritmo en línea . Es un tipo de árbol de búsqueda binaria. Es mejor que el árbol de búsqueda binaria equilibrada de peso fuera de línea, ya que logra una relación competitiva en 
comparación con la relación competitiva del 
árbol de búsqueda binaria equilibrada de peso fuera de línea. Solo se necesitan bits adicionales de memoria en cada Node del árbol para aumentar el rendimiento sobre el árbol de búsqueda binaria balanceada.
El árbol Tango es conceptualmente un árbol de árboles, ya que divide un árbol de búsqueda binaria en caminos preferidos y caminos no preferidos y estos caminos preferidos se almacenan en forma de árboles auxiliares.
Hijo preferido y rutas
preferidas El hijo preferido de cualquier Node del árbol de Tango se define como el hijo tocado más recientemente mediante una técnica de búsqueda de árbol de búsqueda binaria normal. Elaborando más sobre el hijo preferido, supongamos un subárbol T arraigado en el Node n con el hijo derecho como p y el hijo izquierdo como q. Llame a p como el hijo preferido de n si el Node accedido más recientemente del subárbol con raíz en n está presente en el subárbol con raíz en p.
Una ruta preferida se define como la ruta que comienza desde el Node raíz y sigue a todos los hijos preferidos a lo largo de una ruta para llegar a un Node hoja.
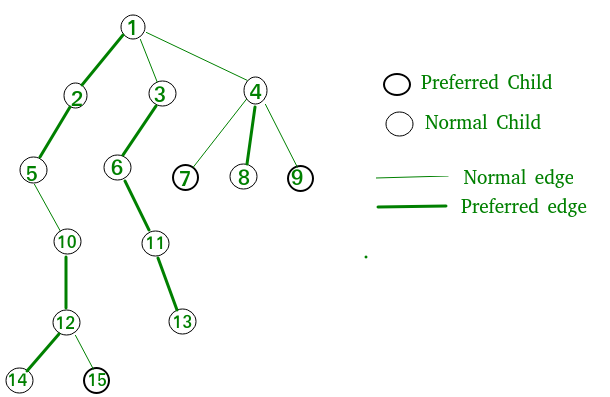
Árbol de Tango
Árboles auxiliares para rutas
preferidas Una ruta preferida se representa almacenando los Nodes de la ruta preferida en un árbol de búsqueda binaria equilibrada, específicamente en un árbol rojo y negro. Entonces, para cada Node no hoja de la ruta P, hay un hijo no preferido 
. Este hijo no preferido actúa como la raíz del nuevo árbol auxiliar y luego adjunta este nuevo árbol auxiliar enraizado en su padre y, de esta manera, es fácil vincular los árboles auxiliares entre sí. También existe la opción de almacenar información adicional en cada Node del árbol auxiliar según nuestras propias necesidades, como la profundidad mínima de los Nodes en el subárbol debajo de él, etc.
Operaciones en Tango Tree
Las dos operaciones más comunes en Tango Trees son Buscar y Actualizar
- Actualización en un árbol de tango
Necesita mantener la estructura del Tango Tree debido a las actualizaciones constantes, ya que el elemento secundario preferido de los Nodes cambia después de cada búsqueda. Cada vez que cambia el preferido, la ruta preferida se divide en dos partes en el Node particular que ha cambiado y la parte superior de la ruta preferida debe unirse al final de otra ruta preferida. Para ello, divida la actualización en dos partes:
- Proceso de corte
- Unirse al proceso
En esta operación, divida la ruta preferida en dos rutas en un Node determinado: la parte superior y la parte inferior. La parte superior es el árbol auxiliar que contiene los Nodes por encima de cierto nivel de Node y la parte inferior se convierte en un árbol auxiliar que contiene el Node por debajo del nivel de Node dado.
En esta operación combinamos los dos árboles auxiliares juntos. Pero solo se pueden combinar si el Node inferior de uno de los árboles combinados es el padre del Node superior del otro árbol combinado. Esta operación de combinación utiliza la operación de concatenación de árboles rojos y negros . Existen dos Nodes en la ruta superior, de modo que se dice que un Node está en la ruta inferior si su valor clave existe entre estos dos Nodes. Para concatenar, simplemente dividimos la ruta superior entre estos dos Nodes y luego unimos los dos árboles auxiliares resultantes a la ruta inferior y nuestro árbol auxiliar resultante está listo.
Para buscar en un árbol de Tango simplemente realizamos la búsqueda en el árbol de búsqueda binaria conceptual. Primero busque la ruta preferida buscando en su árbol auxiliar. Si el Node no se puede encontrar en el árbol auxiliar dado, busque el árbol auxiliar de la siguiente ruta y así sucesivamente hasta que busque en todo el árbol o no pueda encontrar el Node deseado.