Las estructuras de datos son una forma de organizar los datos para que se pueda acceder a ellos de manera más eficiente según la situación. Las estructuras de datos son los fundamentos de cualquier lenguaje de programación alrededor del cual se construye un programa. Python ayuda a aprender lo fundamental de estas estructuras de datos de una manera más sencilla en comparación con otros lenguajes de programación.

En este artículo, discutiremos las estructuras de datos en el lenguaje de programación Python y cómo se relacionan con algunos tipos de datos específicos de Python . Discutiremos todas las estructuras de datos integradas, como listas de tuplas, diccionarios, etc., así como algunas estructuras de datos avanzadas, como árboles, gráficos, etc.
Liza
Las listas de Python son como las arrays, declaradas en otros idiomas, que es una colección ordenada de datos. Es muy flexible ya que no es necesario que los elementos de una lista sean del mismo tipo.
La implementación de Python List es similar a Vectores en C++ o ArrayList en JAVA. La operación costosa es insertar o eliminar el elemento desde el principio de la Lista, ya que todos los elementos deben cambiarse. La inserción y eliminación al final de la lista también puede resultar costosa en el caso de que la memoria preasignada se llene.
Podemos crear una lista en python como se muestra a continuación.
Ejemplo: crear una lista de Python
Python3
List = [1, 2, 3, "GFG", 2.3] print(List)
[1, 2, 3, 'GFG', 2.3]
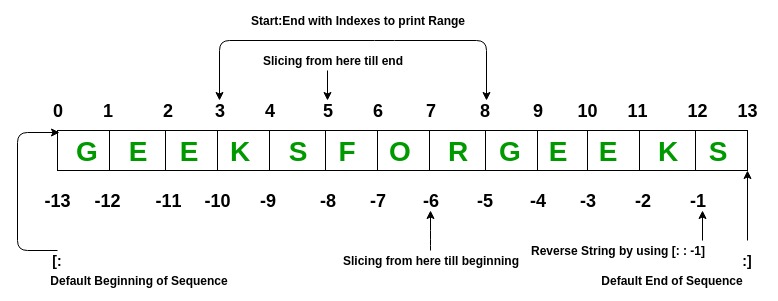
Se puede acceder a los elementos de la lista mediante el índice asignado. En el índice inicial de Python de la lista, la secuencia es 0 y el índice final es (si hay N elementos) N-1.
Ejemplo: operaciones de lista de Python
Python3
# Creating a List with
# the use of multiple values
List = ["Geeks", "For", "Geeks"]
print("\nList containing multiple values: ")
print(List)
# Creating a Multi-Dimensional List
# (By Nesting a list inside a List)
List2 = [['Geeks', 'For'], ['Geeks']]
print("\nMulti-Dimensional List: ")
print(List2)
# accessing a element from the
# list using index number
print("Accessing element from the list")
print(List[0])
print(List[2])
# accessing a element using
# negative indexing
print("Accessing element using negative indexing")
# print the last element of list
print(List[-1])
# print the third last element of list
print(List[-3])
List containing multiple values: ['Geeks', 'For', 'Geeks'] Multi-Dimensional List: [['Geeks', 'For'], ['Geeks']] Accessing element from the list Geeks Geeks Accessing element using negative indexing Geeks Geeks
Diccionario
El diccionario de Python es como tablas hash en cualquier otro idioma con la complejidad de tiempo de O(1). Es una colección desordenada de valores de datos, que se utiliza para almacenar valores de datos como un mapa que, a diferencia de otros tipos de datos que contienen un solo valor como elemento, Dictionary contiene el par clave:valor. El valor-clave se proporciona en el diccionario para hacerlo más optimizado.
La indexación de Python Dictionary se realiza con la ayuda de claves. Estos son de cualquier tipo hashable, es decir, un objeto que nunca puede cambiar como strings, números, tuplas, etc. Podemos crear un diccionario usando llaves ({}) o comprensión de diccionario .
Ejemplo: operaciones de diccionario de Python
Python3
# Creating a Dictionary
Dict = {'Name': 'Geeks', 1: [1, 2, 3, 4]}
print("Creating Dictionary: ")
print(Dict)
# accessing a element using key
print("Accessing a element using key:")
print(Dict['Name'])
# accessing a element using get()
# method
print("Accessing a element using get:")
print(Dict.get(1))
# creation using Dictionary comprehension
myDict = {x: x**2 for x in [1,2,3,4,5]}
print(myDict)
Creating Dictionary:
{'Name': 'Geeks', 1: [1, 2, 3, 4]}
Accessing a element using key:
Geeks
Accessing a element using get:
[1, 2, 3, 4]
{1: 1, 2: 4, 3: 9, 4: 16, 5: 25}
tupla
Python Tuple es una colección de objetos de Python muy parecida a una lista, pero las tuplas son de naturaleza inmutable , es decir, los elementos de la tupla no se pueden agregar ni eliminar una vez creados. Al igual que una Lista, una Tupla también puede contener elementos de varios tipos.
En Python, las tuplas se crean colocando una secuencia de valores separados por ‘comas’ con o sin el uso de paréntesis para agrupar la secuencia de datos.
Nota: Las tuplas también se pueden crear con un solo elemento, pero es un poco complicado. Tener un elemento entre paréntesis no es suficiente, debe haber una ‘coma’ al final para que sea una tupla.
Ejemplo: operaciones de tupla de Python
Python3
# Creating a Tuple with
# the use of Strings
Tuple = ('Geeks', 'For')
print("\nTuple with the use of String: ")
print(Tuple)
# Creating a Tuple with
# the use of list
list1 = [1, 2, 4, 5, 6]
print("\nTuple using List: ")
Tuple = tuple(list1)
# Accessing element using indexing
print("First element of tuple")
print(Tuple[0])
# Accessing element from last
# negative indexing
print("\nLast element of tuple")
print(Tuple[-1])
print("\nThird last element of tuple")
print(Tuple[-3])
Tuple with the use of String:
('Geeks', 'For')
Tuple using List:
First element of tuple
1
Last element of tuple
6
Third last element of tuple
4
Establecer
Python Set es una colección ordenada de datos que es mutable y no permite ningún elemento duplicado. Los conjuntos se utilizan básicamente para incluir pruebas de membresía y eliminar entradas duplicadas. La estructura de datos utilizada en esto es Hashing, una técnica popular para realizar inserción, eliminación y recorrido en O(1) en promedio.
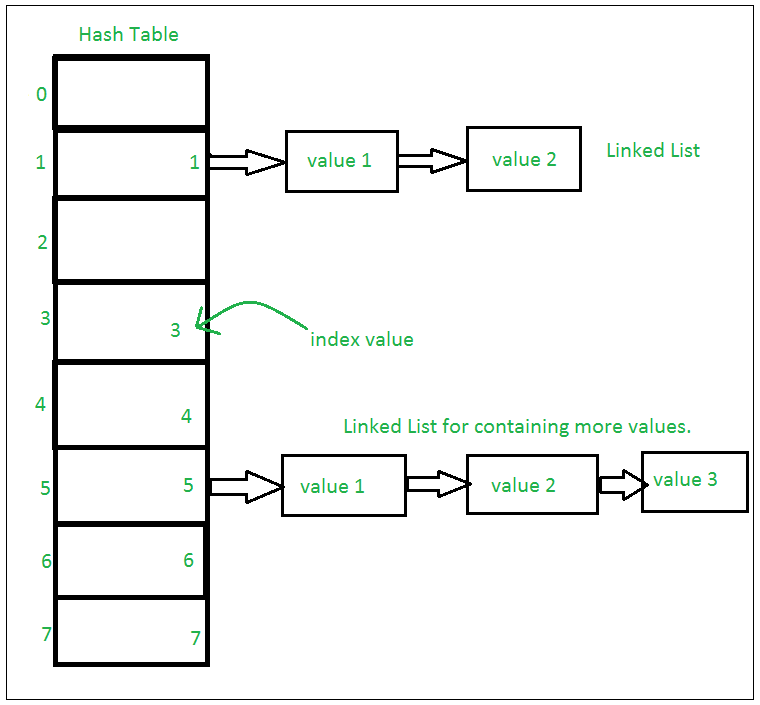
Si hay varios valores presentes en la misma posición de índice, el valor se agrega a esa posición de índice para formar una lista enlazada. En, los conjuntos de CPython se implementan utilizando un diccionario con variables ficticias, donde la clave es el conjunto de miembros con mayores optimizaciones a la complejidad del tiempo.
Establecer implementación:
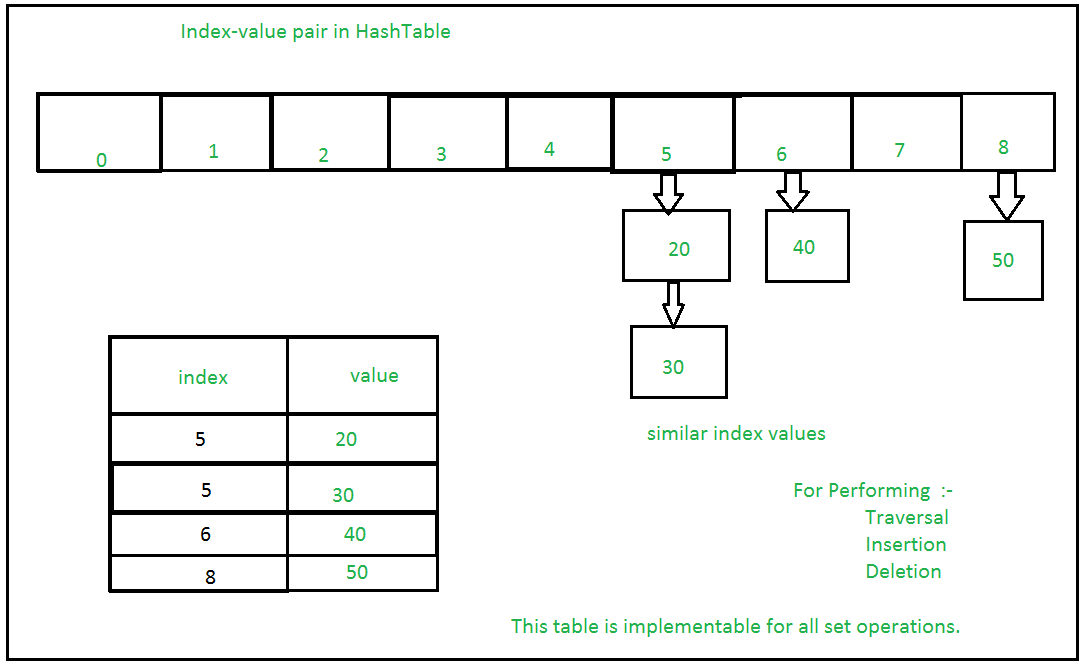
Conjuntos con Numerosas operaciones en una sola HashTable:
Ejemplo: operaciones de conjunto de Python
Python3
# Creating a Set with
# a mixed type of values
# (Having numbers and strings)
Set = set([1, 2, 'Geeks', 4, 'For', 6, 'Geeks'])
print("\nSet with the use of Mixed Values")
print(Set)
# Accessing element using
# for loop
print("\nElements of set: ")
for i in Set:
print(i, end =" ")
print()
# Checking the element
# using in keyword
print("Geeks" in Set)
Set with the use of Mixed Values
{1, 2, 'Geeks', 4, 6, 'For'}
Elements of set:
1 2 Geeks 4 6 For
True
Conjuntos congelados
Los conjuntos congelados en Python son objetos inmutables que solo admiten métodos y operadores que producen un resultado sin afectar el conjunto o conjuntos congelados a los que se aplican. Si bien los elementos de un conjunto se pueden modificar en cualquier momento, los elementos del conjunto congelado siguen siendo los mismos después de la creación.
Si no se pasan parámetros, devuelve un conjunto congelado vacío.
Python3
# Same as {"a", "b","c"}
normal_set = set(["a", "b","c"])
print("Normal Set")
print(normal_set)
# A frozen set
frozen_set = frozenset(["e", "f", "g"])
print("\nFrozen Set")
print(frozen_set)
# Uncommenting below line would cause error as
# we are trying to add element to a frozen set
# frozen_set.add("h")
Normal Set
{'a', 'c', 'b'}
Frozen Set
frozenset({'g', 'e', 'f'})
Cuerda
Python Strings son arrays de bytes que representan caracteres Unicode. En términos más simples, una string es una array inmutable de caracteres. Python no tiene un tipo de datos de caracteres, un solo carácter es simplemente una string con una longitud de 1.
Nota: Como las strings son inmutables, la modificación de una string dará como resultado la creación de una nueva copia.
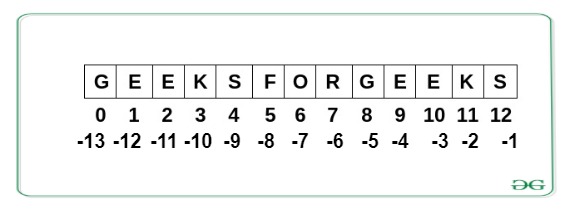
Ejemplo: operaciones de strings de Python
Python3
String = "Welcome to GeeksForGeeks"
print("Creating String: ")
print(String)
# Printing First character
print("\nFirst character of String is: ")
print(String[0])
# Printing Last character
print("\nLast character of String is: ")
print(String[-1])
Creating String: Welcome to GeeksForGeeks First character of String is: W Last character of String is: s
Bytearray
Python Bytearray da una secuencia mutable de enteros en el rango 0 <= x < 256.
Ejemplo: Operaciones Bytearray de Python
Python3
# Creating bytearray
a = bytearray((12, 8, 25, 2))
print("Creating Bytearray:")
print(a)
# accessing elements
print("\nAccessing Elements:", a[1])
# modifying elements
a[1] = 3
print("\nAfter Modifying:")
print(a)
# Appending elements
a.append(30)
print("\nAfter Adding Elements:")
print(a)
Creating Bytearray: bytearray(b'\x0c\x08\x19\x02') Accessing Elements: 8 After Modifying: bytearray(b'\x0c\x03\x19\x02') After Adding Elements: bytearray(b'\x0c\x03\x19\x02\x1e')
ahora hemos estudiado todas las estructuras de datos que vienen integradas en el núcleo de Python. Ahora profundicemos más en Python y veamos el módulo de colecciones que proporciona algunos contenedores que son útiles en muchos casos y brindan más características que las funciones definidas anteriormente.
Módulo de Colecciones
El módulo de recopilación de Python se introdujo para mejorar la funcionalidad de los tipos de datos integrados. Proporciona varios contenedores, veamos cada uno de ellos en detalle.
Contadores
Un contador es una subclase del diccionario. Se utiliza para mantener el recuento de los elementos en un iterable en forma de diccionario desordenado donde la clave representa el elemento en el iterable y el valor representa el recuento de ese elemento en el iterable. Esto es equivalente a una bolsa o multiset de otros idiomas.
Ejemplo: operaciones de contador de Python
Python3
from collections import Counter
# With sequence of items
print(Counter(['B','B','A','B','C','A','B','B','A','C']))
# with dictionary
count = Counter({'A':3, 'B':5, 'C':2})
print(count)
count.update(['A', 1])
print(count)
Counter({'B': 5, 'A': 3, 'C': 2})
Counter({'B': 5, 'A': 3, 'C': 2})
Counter({'B': 5, 'A': 4, 'C': 2, 1: 1})
dictado ordenado
Un OrderedDict también es una subclase de diccionario pero, a diferencia de un diccionario, recuerda el orden en que se insertaron las claves.
Ejemplo: Operaciones Python OrderedDict
Python3
from collections import OrderedDict
print("Before deleting:\n")
od = OrderedDict()
od['a'] = 1
od['b'] = 2
od['c'] = 3
od['d'] = 4
for key, value in od.items():
print(key, value)
print("\nAfter deleting:\n")
od.pop('c')
for key, value in od.items():
print(key, value)
print("\nAfter re-inserting:\n")
od['c'] = 3
for key, value in od.items():
print(key, value)
Before deleting: a 1 b 2 c 3 d 4 After deleting: a 1 b 2 d 4 After re-inserting: a 1 b 2 d 4 c 3
DefaultDict
DefaultDict se usa para proporcionar algunos valores predeterminados para la clave que no existe y nunca genera un KeyError. Sus objetos se pueden inicializar utilizando el método DefaultDict() pasando el tipo de datos como argumento.
Nota: default_factory es una función que proporciona el valor predeterminado para el diccionario creado. Si este parámetro está ausente, se genera KeyError.
Ejemplo: Operaciones Python DefaultDict
Python3
from collections import defaultdict # Defining the dict d = defaultdict(int) L = [1, 2, 3, 4, 2, 4, 1, 2] # Iterate through the list # for keeping the count for i in L: # The default value is 0 # so there is no need to # enter the key first d[i] += 1 print(d)
defaultdict(<class 'int'>, {1: 2, 2: 3, 3: 1, 4: 2})
StringMapa
Un ChainMap encapsula muchos diccionarios en una sola unidad y devuelve una lista de diccionarios. Cuando se necesita encontrar una clave, se busca en todos los diccionarios uno por uno hasta que se encuentra la clave.
Ejemplo: Operaciones Python ChainMap
Python3
from collections import ChainMap
d1 = {'a': 1, 'b': 2}
d2 = {'c': 3, 'd': 4}
d3 = {'e': 5, 'f': 6}
# Defining the chainmap
c = ChainMap(d1, d2, d3)
print(c)
print(c['a'])
print(c['g'])
Producción
ChainMap({'a': 1, 'b': 2}, {'c': 3, 'd': 4}, {'e': 5, 'f': 6})
1
KeyError: 'g'
NamedTuple
Una NamedTuple devuelve un objeto de tupla con nombres para cada posición de la que carecen las tuplas ordinarias. Por ejemplo, considere una tupla que nombra a un estudiante donde el primer elemento representa fname, el segundo representa lname y el tercer elemento representa el DOB. Suponga que para llamar a fname en lugar de recordar la posición del índice, en realidad puede llamar al elemento usando el argumento fname, entonces será muy fácil acceder al elemento de tuplas. Esta funcionalidad la proporciona NamedTuple.
Ejemplo: Operaciones Python NamedTuple
Python3
from collections import namedtuple
# Declaring namedtuple()
Student = namedtuple('Student',['name','age','DOB'])
# Adding values
S = Student('Nandini','19','2541997')
# Access using index
print ("The Student age using index is : ",end ="")
print (S[1])
# Access using name
print ("The Student name using keyname is : ",end ="")
print (S.name)
The Student age using index is : 19 The Student name using keyname is : Nandini
Deque
Deque (Doubly Ended Queue) es la lista optimizada para operaciones de adición y extracción más rápidas desde ambos lados del contenedor. Proporciona una complejidad de tiempo O(1) para las operaciones de adición y extracción en comparación con la lista con complejidad de tiempo O(n).
Python Deque se implementa utilizando listas doblemente enlazadas, por lo que el rendimiento para acceder aleatoriamente a los elementos es O(n).
Ejemplo: operaciones Python Deque
Python3
# importing "collections" for deque operations
import collections
# initializing deque
de = collections.deque([1,2,3])
# using append() to insert element at right end
# inserts 4 at the end of deque
de.append(4)
# printing modified deque
print("The deque after appending at right is : ")
print(de)
# using appendleft() to insert element at left end
# inserts 6 at the beginning of deque
de.appendleft(6)
# printing modified deque
print("The deque after appending at left is : ")
print(de)
# using pop() to delete element from right end
# deletes 4 from the right end of deque
de.pop()
# printing modified deque
print("The deque after deleting from right is : ")
print(de)
# using popleft() to delete element from left end
# deletes 6 from the left end of deque
de.popleft()
# printing modified deque
print("The deque after deleting from left is : ")
print(de)
The deque after appending at right is : deque([1, 2, 3, 4]) The deque after appending at left is : deque([6, 1, 2, 3, 4]) The deque after deleting from right is : deque([6, 1, 2, 3]) The deque after deleting from left is : deque([1, 2, 3])
UserDict
UserDict es un contenedor similar a un diccionario que actúa como un envoltorio alrededor de los objetos del diccionario. Este contenedor se usa cuando alguien quiere crear su propio diccionario con alguna funcionalidad nueva o modificada.
Ejemplo: Python UserDict
Python3
from collections import UserDict
# Creating a Dictionary where
# deletion is not allowed
class MyDict(UserDict):
# Function to stop deletion
# from dictionary
def __del__(self):
raise RuntimeError("Deletion not allowed")
# Function to stop pop from
# dictionary
def pop(self, s = None):
raise RuntimeError("Deletion not allowed")
# Function to stop popitem
# from Dictionary
def popitem(self, s = None):
raise RuntimeError("Deletion not allowed")
# Driver's code
d = MyDict({'a':1,
'b': 2,
'c': 3})
print("Original Dictionary")
print(d)
d.pop(1)
Producción
Original Dictionary
{'a': 1, 'b': 2, 'c': 3}
RuntimeError: Deletion not allowed
Lista de usuarios
UserList es un contenedor similar a una lista que actúa como un envoltorio alrededor de los objetos de la lista. Esto es útil cuando alguien quiere crear su propia lista con alguna funcionalidad modificada o adicional.
Ejemplos: lista de usuarios de Python
Python3
# Python program to demonstrate
# userlist
from collections import UserList
# Creating a List where
# deletion is not allowed
class MyList(UserList):
# Function to stop deletion
# from List
def remove(self, s = None):
raise RuntimeError("Deletion not allowed")
# Function to stop pop from
# List
def pop(self, s = None):
raise RuntimeError("Deletion not allowed")
# Driver's code
L = MyList([1, 2, 3, 4])
print("Original List")
print(L)
# Inserting to List"
L.append(5)
print("After Insertion")
print(L)
# Deleting From List
L.remove()
Producción
Original List [1, 2, 3, 4] After Insertion [1, 2, 3, 4, 5]
RuntimeError: Deletion not allowed
String de usuario
UserString es un contenedor similar a una string y, al igual que UserDict y UserList, actúa como un envoltorio alrededor de los objetos de string. Se usa cuando alguien quiere crear sus propias strings con alguna funcionalidad modificada o adicional.
Ejemplo: string de usuario de Python
Python3
from collections import UserString
# Creating a Mutable String
class Mystring(UserString):
# Function to append to
# string
def append(self, s):
self.data += s
# Function to remove from
# string
def remove(self, s):
self.data = self.data.replace(s, "")
# Driver's code
s1 = Mystring("Geeks")
print("Original String:", s1.data)
# Appending to string
s1.append("s")
print("String After Appending:", s1.data)
# Removing from string
s1.remove("e")
print("String after Removing:", s1.data)
Original String: Geeks String After Appending: Geekss String after Removing: Gkss
Ahora, después de estudiar todas las estructuras de datos, veamos algunas estructuras de datos avanzadas, como pila, cola, gráfico, lista vinculada, etc., que se pueden usar en el lenguaje Python.
Lista enlazada
Una lista enlazada es una estructura de datos lineal, en la que los elementos no se almacenan en ubicaciones de memoria contiguas. Los elementos de una lista vinculada se vinculan mediante punteros como se muestra en la siguiente imagen:
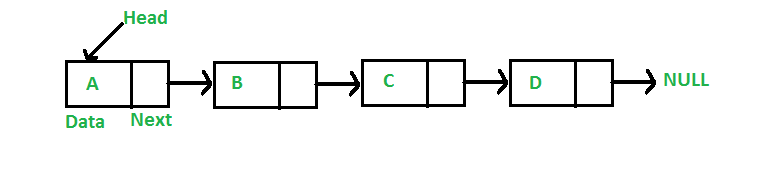
Una lista enlazada se representa mediante un puntero al primer Node de la lista enlazada. El primer Node se llama cabeza. Si la lista enlazada está vacía, entonces el valor de la cabeza es NULL. Cada Node de una lista consta de al menos dos partes:
- Datos
- Puntero (o referencia) al siguiente Node
Ejemplo: definición de lista enlazada en Python
Python3
# Node class class Node: # Function to initialize the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize # next as null # Linked List class class LinkedList: # Function to initialize the Linked # List object def __init__(self): self.head = None
Vamos a crear una lista enlazada simple con 3 Nodes.
Python3
# A simple Python program to introduce a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) ''' Three nodes have been created. We have references to these three blocks as head, second and third llist.head second third | | | | | | +----+------+ +----+------+ +----+------+ | 1 | None | | 2 | None | | 3 | None | +----+------+ +----+------+ +----+------+ ''' llist.head.next = second; # Link first node with second ''' Now next of first Node refers to second. So they both are linked. llist.head second third | | | | | | +----+------+ +----+------+ +----+------+ | 1 | o-------->| 2 | null | | 3 | null | +----+------+ +----+------+ +----+------+ ''' second.next = third; # Link second node with the third node ''' Now next of second Node refers to third. So all three nodes are linked. llist.head second third | | | | | | +----+------+ +----+------+ +----+------+ | 1 | o-------->| 2 | o-------->| 3 | null | +----+------+ +----+------+ +----+------+ '''
Recorrido de lista enlazada
En el programa anterior, hemos creado una lista enlazada simple con tres Nodes. Recorramos la lista creada e imprimamos los datos de cada Node. Para el recorrido, escribamos una función de propósito general printList() que imprima cualquier lista dada.
Python3
# A simple Python program for traversal of a linked list # Node class class Node: # Function to initialise the node object def __init__(self, data): self.data = data # Assign data self.next = None # Initialize next as null # Linked List class contains a Node object class LinkedList: # Function to initialize head def __init__(self): self.head = None # This function prints contents of linked list # starting from head def printList(self): temp = self.head while (temp): print (temp.data) temp = temp.next # Code execution starts here if __name__=='__main__': # Start with the empty list llist = LinkedList() llist.head = Node(1) second = Node(2) third = Node(3) llist.head.next = second; # Link first node with second second.next = third; # Link second node with the third node llist.printList()
1 2 3
Pila
Una pila es una estructura de datos lineal que almacena elementos en forma de último en entrar/primero en salir (LIFO) o primero en entrar/último en salir (FILO). En la pila, se agrega un nuevo elemento en un extremo y se elimina un elemento solo de ese extremo. Las operaciones de inserción y eliminación a menudo se denominan empujar y sacar.
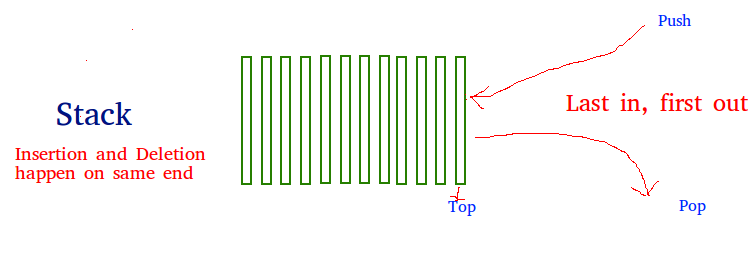
Las funciones asociadas con la pila son:
- vacío() – Devuelve si la pila está vacía – Complejidad de tiempo: O (1)
- size() – Devuelve el tamaño de la pila – Complejidad de tiempo: O(1)
- top() – Devuelve una referencia al elemento superior de la pila – Complejidad de tiempo: O (1)
- push(a) – Inserta el elemento ‘a’ en la parte superior de la pila – Complejidad de tiempo: O(1)
- pop() – Elimina el elemento superior de la pila – Complejidad de tiempo: O (1)
Implementación de la pila de Python
Stack en Python se puede implementar de las siguientes maneras:
- lista
- Colecciones.deque
- cola.LifoQueue
Implementación usando Lista
La lista de estructura de datos incorporada de Python se puede usar como una pila. En lugar de push(), append() se usa para agregar elementos a la parte superior de la pila, mientras que pop() elimina el elemento en orden LIFO.
Python3
stack = []
# append() function to push
# element in the stack
stack.append('g')
stack.append('f')
stack.append('g')
print('Initial stack')
print(stack)
# pop() function to pop
# element from stack in
# LIFO order
print('\nElements popped from stack:')
print(stack.pop())
print(stack.pop())
print(stack.pop())
print('\nStack after elements are popped:')
print(stack)
# uncommenting print(stack.pop())
# will cause an IndexError
# as the stack is now empty
Initial stack ['g', 'f', 'g'] Elements popped from stack: g f g Stack after elements are popped: []
Implementación usando collections.deque:
La pila de Python se puede implementar usando la clase deque del módulo de colecciones. Deque es preferible a la lista en los casos en los que necesitamos operaciones de adición y extracción más rápidas desde ambos extremos del contenedor, ya que deque proporciona una complejidad de tiempo O(1) para las operaciones de adición y extracción en comparación con la lista que proporciona O(n) complejidad del tiempo.
Python3
from collections import deque
stack = deque()
# append() function to push
# element in the stack
stack.append('g')
stack.append('f')
stack.append('g')
print('Initial stack:')
print(stack)
# pop() function to pop
# element from stack in
# LIFO order
print('\nElements popped from stack:')
print(stack.pop())
print(stack.pop())
print(stack.pop())
print('\nStack after elements are popped:')
print(stack)
# uncommenting print(stack.pop())
# will cause an IndexError
# as the stack is now empty
Initial stack: deque(['g', 'f', 'g']) Elements popped from stack: g f g Stack after elements are popped: deque([])
Implementación utilizando el módulo de cola
El módulo de cola también tiene una cola LIFO, que es básicamente una pila. Los datos se insertan en la cola usando la función put() y get() saca los datos de la cola.
Python3
from queue import LifoQueue
# Initializing a stack
stack = LifoQueue(maxsize = 3)
# qsize() show the number of elements
# in the stack
print(stack.qsize())
# put() function to push
# element in the stack
stack.put('g')
stack.put('f')
stack.put('g')
print("Full: ", stack.full())
print("Size: ", stack.qsize())
# get() function to pop
# element from stack in
# LIFO order
print('\nElements popped from the stack')
print(stack.get())
print(stack.get())
print(stack.get())
print("\nEmpty: ", stack.empty())
0 Full: True Size: 3 Elements popped from the stack g f g Empty: True
Cola
Como una pila, la cola es una estructura de datos lineal que almacena elementos en forma de primero en entrar, primero en salir (FIFO). Con una cola, el elemento agregado menos recientemente se elimina primero. Un buen ejemplo de la cola es cualquier cola de consumidores de un recurso donde se atiende primero al consumidor que llegó primero.
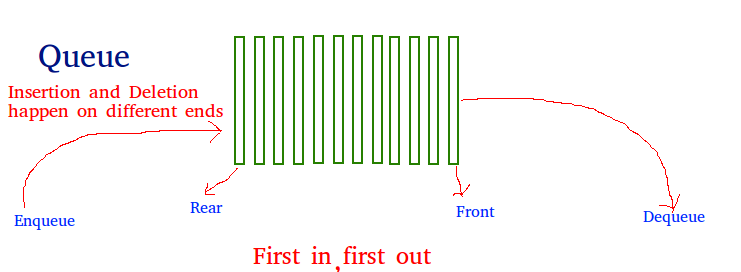
Las operaciones asociadas con la cola son:
- Poner en cola: agrega un elemento a la cola. Si la cola está llena, se dice que es una condición de desbordamiento – Complejidad de tiempo: O(1)
- Dequeue: elimina un elemento de la cola. Los elementos se abren en el mismo orden en que se empujan. Si la cola está vacía, se dice que es una condición de subdesbordamiento – Complejidad de tiempo: O(1)
- Anverso: Obtener el elemento frontal de la cola – Complejidad de tiempo: O(1)
- Posterior: obtenga el último elemento de la cola – Complejidad de tiempo: O (1)
Implementación de la cola de Python
La cola en Python se puede implementar de las siguientes maneras:
- lista
- colecciones.deque
- cola.Cola
Implementación usando lista
En lugar de enqueue() y dequeue(), se utilizan las funciones append() y pop().
Python3
# Initializing a queue
queue = []
# Adding elements to the queue
queue.append('g')
queue.append('f')
queue.append('g')
print("Initial queue")
print(queue)
# Removing elements from the queue
print("\nElements dequeued from queue")
print(queue.pop(0))
print(queue.pop(0))
print(queue.pop(0))
print("\nQueue after removing elements")
print(queue)
# Uncommenting print(queue.pop(0))
# will raise and IndexError
# as the queue is now empty
Initial queue ['g', 'f', 'g'] Elements dequeued from queue g f g Queue after removing elements []
Implementación usando collections.deque
Deque es preferible a la lista en los casos en los que necesitamos operaciones de adición y extracción más rápidas desde ambos extremos del contenedor, ya que deque proporciona una complejidad de tiempo O(1) para las operaciones de adición y extracción en comparación con la lista que proporciona O(n) complejidad del tiempo.
Python3
from collections import deque
# Initializing a queue
q = deque()
# Adding elements to a queue
q.append('g')
q.append('f')
q.append('g')
print("Initial queue")
print(q)
# Removing elements from a queue
print("\nElements dequeued from the queue")
print(q.popleft())
print(q.popleft())
print(q.popleft())
print("\nQueue after removing elements")
print(q)
# Uncommenting q.popleft()
# will raise an IndexError
# as queue is now empty
Initial queue deque(['g', 'f', 'g']) Elements dequeued from the queue g f g Queue after removing elements deque([])
Implementación utilizando la cola.Cola
queue.Queue(maxsize) inicializa una variable a un tamaño máximo de maxsize. Un tamaño máximo de cero ‘0’ significa una cola infinita. Esta cola sigue la regla FIFO.
Python3
from queue import Queue
# Initializing a queue
q = Queue(maxsize = 3)
# qsize() give the maxsize
# of the Queue
print(q.qsize())
# Adding of element to queue
q.put('g')
q.put('f')
q.put('g')
# Return Boolean for Full
# Queue
print("\nFull: ", q.full())
# Removing element from queue
print("\nElements dequeued from the queue")
print(q.get())
print(q.get())
print(q.get())
# Return Boolean for Empty
# Queue
print("\nEmpty: ", q.empty())
q.put(1)
print("\nEmpty: ", q.empty())
print("Full: ", q.full())
# This would result into Infinite
# Loop as the Queue is empty.
# print(q.get())
0 Full: True Elements dequeued from the queue g f g Empty: True Empty: False Full: False
cola de prioridad
Las colas de prioridad son estructuras de datos abstractas en las que cada dato/valor de la cola tiene una determinada prioridad. Por ejemplo, en las aerolíneas, el equipaje con título “Business” o “First-class” llega antes que el resto. Priority Queue es una extensión de la cola con las siguientes propiedades.
- Un elemento con prioridad alta se elimina de la cola antes que un elemento con prioridad baja.
- Si dos elementos tienen la misma prioridad, se sirven según su orden en la cola.
Python3
# A simple implementation of Priority Queue # using Queue. class PriorityQueue(object): def __init__(self): self.queue = [] def __str__(self): return ' '.join([str(i) for i in self.queue]) # for checking if the queue is empty def isEmpty(self): return len(self.queue) == 0 # for inserting an element in the queue def insert(self, data): self.queue.append(data) # for popping an element based on Priority def delete(self): try: max = 0 for i in range(len(self.queue)): if self.queue[i] > self.queue[max]: max = i item = self.queue[max] del self.queue[max] return item except IndexError: print() exit() if __name__ == '__main__': myQueue = PriorityQueue() myQueue.insert(12) myQueue.insert(1) myQueue.insert(14) myQueue.insert(7) print(myQueue) while not myQueue.isEmpty(): print(myQueue.delete())
12 1 14 7 14 12 7 1
Cola de montón (o heapq)
El módulo heapq en Python proporciona la estructura de datos del montón que se usa principalmente para representar una cola de prioridad. La propiedad de esta estructura de datos en Python es que cada vez que se extrae el elemento de montón más pequeño (min-heap). Cada vez que se empujan o extraen elementos, se mantiene la estructura del montón. El elemento heap[0] también devuelve el elemento más pequeño cada vez.
Soporta la extracción e inserción del elemento más pequeño en los tiempos O(log n).
Python3
# importing "heapq" to implement heap queue
import heapq
# initializing list
li = [5, 7, 9, 1, 3]
# using heapify to convert list into heap
heapq.heapify(li)
# printing created heap
print ("The created heap is : ",end="")
print (list(li))
# using heappush() to push elements into heap
# pushes 4
heapq.heappush(li,4)
# printing modified heap
print ("The modified heap after push is : ",end="")
print (list(li))
# using heappop() to pop smallest element
print ("The popped and smallest element is : ",end="")
print (heapq.heappop(li))
The created heap is : [1, 3, 9, 7, 5] The modified heap after push is : [1, 3, 4, 7, 5, 9] The popped and smallest element is : 1
Árbol binario
Un árbol es una estructura de datos jerárquica que se parece a la siguiente figura:
tree
----
j <-- root
/ \
f k
/ \ \
a h z <-- leaves
El Node superior del árbol se denomina raíz, mientras que los Nodes inferiores o los Nodes sin hijos se denominan Nodes hoja. Los Nodes que están directamente debajo de un Node se llaman sus hijos y los Nodes que están directamente encima de algo se llaman su padre.
Un árbol binario es un árbol cuyos elementos pueden tener casi dos hijos. Dado que cada elemento en un árbol binario puede tener solo 2 hijos, normalmente los llamamos los hijos izquierdo y derecho. Un Node de árbol binario contiene las siguientes partes.
- Datos
- Puntero al niño izquierdo
- Puntero al niño derecho
Ejemplo: definición de clase de Node
Python3
# A Python class that represents an individual node # in a Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key
Ahora vamos a crear un árbol con 4 Nodes en Python. Supongamos que la estructura de árbol se ve a continuación:
tree
----
1 <-- root
/ \
2 3
/
4
Ejemplo: agregar datos al árbol
Python3
# Python program to introduce Binary Tree # A class that represents an individual node in a # Binary Tree class Node: def __init__(self,key): self.left = None self.right = None self.val = key # create root root = Node(1) ''' following is the tree after above statement 1 / \ None None''' root.left = Node(2); root.right = Node(3); ''' 2 and 3 become left and right children of 1 1 / \ 2 3 / \ / \ None None None None''' root.left.left = Node(4); '''4 becomes left child of 2 1 / \ 2 3 / \ / \ 4 None None None / \ None None'''
Árbol transversal
Los árboles se pueden atravesar de diferentes maneras. Las siguientes son las formas generalmente utilizadas para atravesar árboles. Consideremos el siguiente árbol:
tree
----
1 <-- root
/ \
2 3
/ \
4 5
Primeros recorridos de profundidad:
- En orden (Izquierda, Raíz, Derecha): 4 2 5 1 3
- Pedido anticipado (Raíz, Izquierda, Derecha): 1 2 4 5 3
- Orden posterior (izquierda, derecha, raíz): 4 5 2 3 1
Algoritmo en orden (árbol)
- Atraviese el subárbol izquierdo, es decir, llame a Inorder (subárbol izquierdo)
- Visita la raíz.
- Atraviese el subárbol derecho, es decir, llame a Inorder (subárbol derecho)
Preorden del algoritmo (árbol)
- Visita la raíz.
- Atraviese el subárbol izquierdo, es decir, llame a Preordenar (subárbol izquierdo)
- Atraviese el subárbol derecho, es decir, llame a Preordenar (subárbol derecho)
Postorden del algoritmo (árbol)
- Atraviese el subárbol izquierdo, es decir, llame a Postorder (subárbol izquierdo)
- Atraviese el subárbol derecho, es decir, llame a Postorder (subárbol derecho)
- Visita la raíz.
Python3
# Python program to for tree traversals
# A class that represents an individual node in a
# Binary Tree
class Node:
def __init__(self, key):
self.left = None
self.right = None
self.val = key
# A function to do inorder tree traversal
def printInorder(root):
if root:
# First recur on left child
printInorder(root.left)
# then print the data of node
print(root.val),
# now recur on right child
printInorder(root.right)
# A function to do postorder tree traversal
def printPostorder(root):
if root:
# First recur on left child
printPostorder(root.left)
# the recur on right child
printPostorder(root.right)
# now print the data of node
print(root.val),
# A function to do preorder tree traversal
def printPreorder(root):
if root:
# First print the data of node
print(root.val),
# Then recur on left child
printPreorder(root.left)
# Finally recur on right child
printPreorder(root.right)
# Driver code
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print("Preorder traversal of binary tree is")
printPreorder(root)
print("\nInorder traversal of binary tree is")
printInorder(root)
print("\nPostorder traversal of binary tree is")
printPostorder(root)
Preorder traversal of binary tree is 1 2 4 5 3 Inorder traversal of binary tree is 4 2 5 1 3 Postorder traversal of binary tree is 4 5 2 3 1
Complejidad del tiempo – O(n)
Recorrido de orden primero en amplitud o de nivel
El recorrido de orden de nivel de un árbol es el recorrido primero en anchura para el árbol. El recorrido de orden de nivel del árbol anterior es 1 2 3 4 5.
Para cada Node, primero, se visita el Node y luego sus Nodes secundarios se colocan en una cola FIFO. A continuación se muestra el algoritmo para el mismo:
- Crear una cola vacía q
- temp_node = root /*comenzar desde la raíz*/
- Bucle mientras temp_node no es NULL
- imprimir temp_node->datos.
- Poner en cola a los hijos de temp_node (primero a la izquierda y luego a la derecha) a q
- Eliminar de la cola un Node de q
Python3
# Python program to print level
# order traversal using Queue
# A node structure
class Node:
# A utility function to create a new node
def __init__(self ,key):
self.data = key
self.left = None
self.right = None
# Iterative Method to print the
# height of a binary tree
def printLevelOrder(root):
# Base Case
if root is None:
return
# Create an empty queue
# for level order traversal
queue = []
# Enqueue Root and initialize height
queue.append(root)
while(len(queue) > 0):
# Print front of queue and
# remove it from queue
print (queue[0].data)
node = queue.pop(0)
# Enqueue left child
if node.left is not None:
queue.append(node.left)
# Enqueue right child
if node.right is not None:
queue.append(node.right)
# Driver Program to test above function
root = Node(1)
root.left = Node(2)
root.right = Node(3)
root.left.left = Node(4)
root.left.right = Node(5)
print ("Level Order Traversal of binary tree is -")
printLevelOrder(root)
Level Order Traversal of binary tree is - 1 2 3 4 5
Complejidad de tiempo: O(n)
Grafico
Un gráfico es una estructura de datos no lineal que consta de Nodes y bordes. Los Nodes a veces también se conocen como vértices y los bordes son líneas o arcos que conectan dos Nodes en el gráfico. Más formalmente, un gráfico se puede definir como un gráfico que consta de un conjunto finito de vértices (o Nodes) y un conjunto de aristas que conectan un par de Nodes.
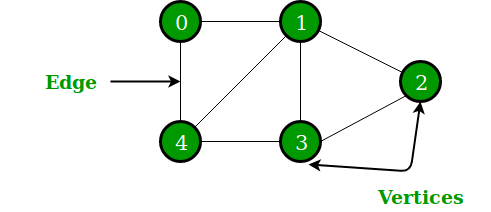
En el gráfico anterior, el conjunto de vértices V = {0,1,2,3,4} y el conjunto de aristas E = {01, 12, 23, 34, 04, 14, 13}.
Las dos siguientes son las representaciones más utilizadas de un gráfico.
- Array de adyacencia
- Lista de adyacencia
Array de adyacencia
Adjacency Matrix es una array 2D de tamaño V x V donde V es el número de vértices en un gráfico. Sea la array 2D adj[][], una ranura adj[i][j] = 1 indica que hay una arista desde el vértice i hasta el vértice j. La array de adyacencia para un gráfico no dirigido siempre es simétrica. La array de adyacencia también se utiliza para representar gráficos ponderados. Si adj[i][j] = w, entonces hay una arista del vértice i al vértice j con peso w.
Python3
# A simple representation of graph using Adjacency Matrix
class Graph:
def __init__(self,numvertex):
self.adjMatrix = [[-1]*numvertex for x in range(numvertex)]
self.numvertex = numvertex
self.vertices = {}
self.verticeslist =[0]*numvertex
def set_vertex(self,vtx,id):
if 0<=vtx<=self.numvertex:
self.vertices[id] = vtx
self.verticeslist[vtx] = id
def set_edge(self,frm,to,cost=0):
frm = self.vertices[frm]
to = self.vertices[to]
self.adjMatrix[frm][to] = cost
# for directed graph do not add this
self.adjMatrix[to][frm] = cost
def get_vertex(self):
return self.verticeslist
def get_edges(self):
edges=[]
for i in range (self.numvertex):
for j in range (self.numvertex):
if (self.adjMatrix[i][j]!=-1):
edges.append((self.verticeslist[i],self.verticeslist[j],self.adjMatrix[i][j]))
return edges
def get_matrix(self):
return self.adjMatrix
G =Graph(6)
G.set_vertex(0,'a')
G.set_vertex(1,'b')
G.set_vertex(2,'c')
G.set_vertex(3,'d')
G.set_vertex(4,'e')
G.set_vertex(5,'f')
G.set_edge('a','e',10)
G.set_edge('a','c',20)
G.set_edge('c','b',30)
G.set_edge('b','e',40)
G.set_edge('e','d',50)
G.set_edge('f','e',60)
print("Vertices of Graph")
print(G.get_vertex())
print("Edges of Graph")
print(G.get_edges())
print("Adjacency Matrix of Graph")
print(G.get_matrix())
Producción
Vértices del gráfico
[‘a B C D e F’]
Bordes del gráfico
[(‘a’, ‘c’, 20), (‘a’, ‘e’, 10), (‘b’, ‘c’, 30), (‘b’, ‘e’, 40), ( ‘c’, ‘a’, 20), (‘c’, ‘b’, 30), (‘d’, ‘e’, 50), (‘e’, ‘a’, 10), (‘e ‘, ‘b’, 40), (‘e’, ‘d’, 50), (‘e’, ‘f’, 60), (‘f’, ‘e’, 60)]
Array de adyacencia de gráfico
[[-1, -1, 20, -1, 10, -1], [-1, -1, 30, -1, 40, -1], [20, 30, -1, -1, -1 , -1], [-1, -1, -1, -1, 50, -1], [10, 40, -1, 50, -1, 60], [-1, -1, -1, -1, 60, -1]]
Lista de adyacencia
Se utiliza una array de listas. El tamaño de la array es igual al número de vértices. Sea el arreglo un arreglo[]. Una array de entrada[i] representa la lista de vértices adyacentes al i-ésimo vértice. Esta representación también se puede utilizar para representar un gráfico ponderado. Los pesos de los bordes se pueden representar como listas de pares. A continuación se muestra la representación de la lista de adyacencia del gráfico anterior.

Python3
# A class to represent the adjacency list of the node
class AdjNode:
def __init__(self, data):
self.vertex = data
self.next = None
# A class to represent a graph. A graph
# is the list of the adjacency lists.
# Size of the array will be the no. of the
# vertices "V"
class Graph:
def __init__(self, vertices):
self.V = vertices
self.graph = [None] * self.V
# Function to add an edge in an undirected graph
def add_edge(self, src, dest):
# Adding the node to the source node
node = AdjNode(dest)
node.next = self.graph[src]
self.graph[src] = node
# Adding the source node to the destination as
# it is the undirected graph
node = AdjNode(src)
node.next = self.graph[dest]
self.graph[dest] = node
# Function to print the graph
def print_graph(self):
for i in range(self.V):
print("Adjacency list of vertex {}\n head".format(i), end="")
temp = self.graph[i]
while temp:
print(" -> {}".format(temp.vertex), end="")
temp = temp.next
print(" \n")
# Driver program to the above graph class
if __name__ == "__main__":
V = 5
graph = Graph(V)
graph.add_edge(0, 1)
graph.add_edge(0, 4)
graph.add_edge(1, 2)
graph.add_edge(1, 3)
graph.add_edge(1, 4)
graph.add_edge(2, 3)
graph.add_edge(3, 4)
graph.print_graph()
Adjacency list of vertex 0 head -> 4 -> 1 Adjacency list of vertex 1 head -> 4 -> 3 -> 2 -> 0 Adjacency list of vertex 2 head -> 3 -> 1 Adjacency list of vertex 3 head -> 4 -> 2 -> 1 Adjacency list of vertex 4 head -> 3 -> 1 -> 0
Gráfico transversal
Búsqueda primero en amplitud o BFS
El recorrido primero en anchura de un gráfico es similar al recorrido primero en anchura de un árbol. El único inconveniente aquí es que, a diferencia de los árboles, los gráficos pueden contener ciclos, por lo que podemos volver al mismo Node. Para evitar procesar un Node más de una vez, usamos una array visitada booleana. Para simplificar, se supone que todos los vértices son accesibles desde el vértice inicial.
Por ejemplo, en el siguiente gráfico, comenzamos el recorrido desde el vértice 2. Cuando llegamos al vértice 0, buscamos todos los vértices adyacentes. 2 también es un vértice adyacente de 0. Si no marcamos los vértices visitados, entonces 2 se procesará nuevamente y se convertirá en un proceso sin terminación. Un recorrido primero en amplitud del siguiente gráfico es 2, 0, 3, 1.
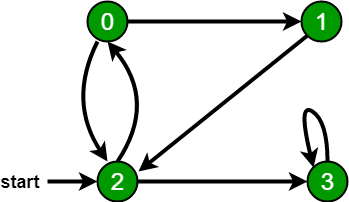
Python3
# Python3 Program to print BFS traversal
# from a given source vertex. BFS(int s)
# traverses vertices reachable from s.
from collections import defaultdict
# This class represents a directed graph
# using adjacency list representation
class Graph:
# Constructor
def __init__(self):
# default dictionary to store graph
self.graph = defaultdict(list)
# function to add an edge to graph
def addEdge(self,u,v):
self.graph[u].append(v)
# Function to print a BFS of graph
def BFS(self, s):
# Mark all the vertices as not visited
visited = [False] * (max(self.graph) + 1)
# Create a queue for BFS
queue = []
# Mark the source node as
# visited and enqueue it
queue.append(s)
visited[s] = True
while queue:
# Dequeue a vertex from
# queue and print it
s = queue.pop(0)
print (s, end = " ")
# Get all adjacent vertices of the
# dequeued vertex s. If a adjacent
# has not been visited, then mark it
# visited and enqueue it
for i in self.graph[s]:
if visited[i] == False:
queue.append(i)
visited[i] = True
# Driver code
# Create a graph given in
# the above diagram
g = Graph()
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(2, 3)
g.addEdge(3, 3)
print ("Following is Breadth First Traversal"
" (starting from vertex 2)")
g.BFS(2)
# This code is contributed by Neelam Yadav
Following is Breadth First Traversal (starting from vertex 2) 2 0 3 1
Complejidad temporal: O(V+E) donde V es el número de vértices del gráfico y E es el número de aristas del gráfico.
Primera búsqueda en profundidad o DFS
El primer recorrido en profundidad de un gráfico es similar al primer recorrido en profundidad de un árbol. El único inconveniente aquí es que, a diferencia de los árboles, los gráficos pueden contener ciclos, un Node puede visitarse dos veces. Para evitar procesar un Node más de una vez, use una array visitada booleana.
Algoritmo:
- Cree una función recursiva que tome el índice del Node y una array visitada.
- Marque el Node actual como visitado e imprima el Node.
- Recorra todos los Nodes adyacentes y sin marcar y llame a la función recursiva con el índice del Node adyacente.
Python3
# Python3 program to print DFS traversal
# from a given graph
from collections import defaultdict
# This class represents a directed graph using
# adjacency list representation
class Graph:
# Constructor
def __init__(self):
# default dictionary to store graph
self.graph = defaultdict(list)
# function to add an edge to graph
def addEdge(self, u, v):
self.graph[u].append(v)
# A function used by DFS
def DFSUtil(self, v, visited):
# Mark the current node as visited
# and print it
visited.add(v)
print(v, end=' ')
# Recur for all the vertices
# adjacent to this vertex
for neighbour in self.graph[v]:
if neighbour not in visited:
self.DFSUtil(neighbour, visited)
# The function to do DFS traversal. It uses
# recursive DFSUtil()
def DFS(self, v):
# Create a set to store visited vertices
visited = set()
# Call the recursive helper function
# to print DFS traversal
self.DFSUtil(v, visited)
# Driver code
# Create a graph given
# in the above diagram
g = Graph()
g.addEdge(0, 1)
g.addEdge(0, 2)
g.addEdge(1, 2)
g.addEdge(2, 0)
g.addEdge(2, 3)
g.addEdge(3, 3)
print("Following is DFS from (starting from vertex 2)")
g.DFS(2)
Following is DFS from (starting from vertex 2) 2 0 1 3
Complejidad temporal: O(V + E), donde V es el número de vértices y E es el número de aristas del grafo.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
