Estructuras de datos y algoritmos | Conjunto 26

Las siguientes preguntas se han hecho en el examen GATE 2011.

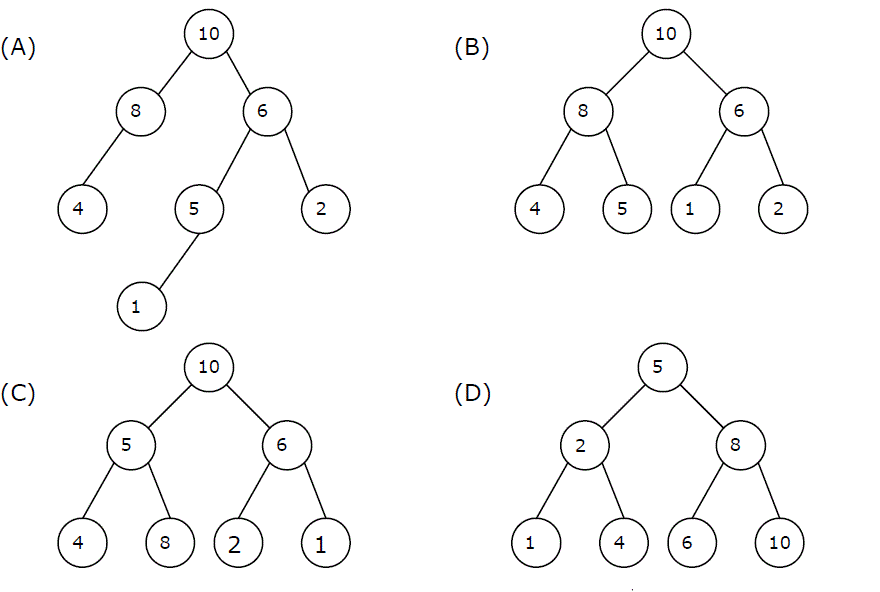
1) Un montón máximo es un montón donde el valor de cada padre es mayor o igual que los valores de sus hijos. ¿Cuál de los siguientes es un montón máximo?

Respuesta: (B)
Un árbol binario es max-heap si es un árbol binario completo (un árbol binario completo es un árbol binario en el que todos los niveles, excepto posiblemente el último, están completamente llenos, y todos los Nodes están tan a la izquierda como sea posible). posible) y sigue la propiedad max-heap (el valor de cada padre es mayor o igual que los valores de sus hijos).

A) no es un montón máximo porque no es un árbol binario completo
B) es un montón máximo porque es un árbol binario completo y sigue la propiedad de montón máximo.
C) no es un montón máximo porque 8 es un chile de 5 en este árbol, por lo que viola la propiedad de montón máximo.
D) no es un montón máximo porque 8 es un chile de 5 en este árbol, por lo que viola la propiedad de montón máximo. Hay muchos otros Nodes en este árbol que violan la propiedad max-heap en este árbol.

2) Cuatro arrays M1, M2, M3 y M4 de dimensiones pxq, qxr, rxs y sxt respectivamente se pueden multiplicar de varias maneras con diferente número de multiplicaciones escalares totales. Por ejemplo, cuando se multiplica como ((M1 X M2) X (M3 X M4)), el número total de multiplicaciones es pqr + rst + prt. Cuando se multiplica como (((M1 X M2) X M3) X M4), el número total de multiplicaciones escalares es pqr + prs + pst.

Si p = 10, q = 100, r = 20, s = 5 y t = 80, entonces el número de multiplicaciones escalares necesarias es
A) 248000
B) 44000
C) 19000
D) 25000

Respuesta (C)
Obtenemos el número mínimo de multiplicaciones usando ((M1 X (M2 X M3)) X M4).

Número total de multiplicaciones = 100x20x5 (para M2 x M3) + 10x100x5 + 10x5x80 = 19000.

3) ¿Cuál de las opciones dadas proporciona el orden creciente de complejidad asintótica de las funciones f1, f2, f3 y f4?

f1(n) = 2^n
f2(n) = n^(3/2)
f3(n) = nLogn
f4(n) = n^(Logn)

A) f3, f2, f4, f1
B) f3, f2, f1, f4
C) f2, f3, f1, f4
D) f2, f3, f4, f1

Respuesta (A)
Consulte http://geeksquiz.com/algorithms-analysis-of-algorithms-question-9/ para obtener una explicación.

4) Nos dan un conjunto de n elementos distintos y un árbol binario sin etiquetar con n Nodes. ¿De cuántas maneras podemos poblar el árbol con el conjunto dado para que se convierta en un árbol de búsqueda binaria?
A) 0
B) 1
C) n!
D) (1/(n+1)).2nCn

Respuesta (B)

Ver esta explicación de PeddaBoku.

5) A continuación se proporciona un algoritmo para encontrar la longitud de la secuencia de números monótonamente creciente más larga en una array A[0 :n-1].
Sea Li la longitud de la secuencia monótonamente creciente más larga que comienza en el índice i de la array.
¿Cuál de las siguientes afirmaciones es VERDADERA? (A) El algoritmo usa un paradigma de programación dinámica (B) El algoritmo tiene una complejidad lineal y usa un paradigma de bifurcación y límite (C) El algoritmo tiene una complejidad polinomial no lineal y usa un paradigma de bifurcación y límite (D) El algoritmo usa división y conquistar el paradigma.

Respuesta: (A)

Consulte GATE Corner para ver todos los documentos/soluciones/explicaciones del año anterior, programa de estudios, fechas importantes, notas, etc.

Escriba comentarios si encuentra que alguna de las respuestas/explicaciones es incorrecta, o si desea compartir más información sobre los temas discutidos anteriormente.