Estructuras de datos y algoritmos | Conjunto 32

Se han hecho las siguientes preguntas en el examen GATE CS 2014.

1) Sea G un grafo con n vértices y m aristas. ¿Cuál es el límite superior más ajustado en el tiempo de ejecución en la primera búsqueda en profundidad de G? Suponga que el gráfico se representa utilizando una array de adyacencia.
(A) O(n)
(B) O(m+n)
(C) O(n ² )
(D) O(mn)

Respuesta: (C)
Explicación: La búsqueda en profundidad de un gráfico toma O(m+n) tiempo cuando el gráfico se representa usando una lista de adyacencia.

En la representación de array de adyacencia, el gráfico se representa como una array «nxn». Para hacer DFS, para cada vértice, recorremos la fila correspondiente a ese vértice para encontrar todos los vértices adyacentes (en la representación de lista de adyacencia, recorremos solo los vértices adyacentes del vértice). Por lo tanto, la complejidad del tiempo se convierte en O(n ² )

2) Considere un árbol binario enraizado representado mediante punteros. El mejor límite superior del tiempo requerido para determinar el número de subárboles que tienen exactamente 4 Nodes O(n ^a Logn ^b ). Entonces el valor de a + 10b es ________

Respuesta: 1
Explicación: Podemos encontrar el subárbol con 4 Nodes en tiempo O(n). El siguiente puede ser un enfoque simple.
1) Atraviese el árbol de abajo hacia arriba y encuentre el tamaño del subárbol enraizado con el Node actual
2) Si el tamaño se convierte en 4, imprima el Node actual.

int print4Subtree(struct Node *root)
{
    if (root == NULL)
      return 0;
    int l =  print4Subtree(root->left);
    int r =   print4Subtree(root->right);
    if ((l + r + 1) == 4)
       printf("%d ", root->data);
    return (l + r + 1);
}

3) Considere el gráfico dirigido que se muestra a continuación. ¿Cuál de las siguientes es VERDADERA?

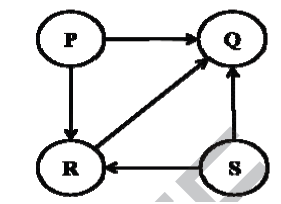
(A) El gráfico no tiene ningún ordenamiento topológico
(B) Tanto PQRS como SRPQ son ordenamiento topológico
(C) Tanto PSRQ como SPRQ son ordenamiento topológico
(D) PSRQ es el único ordenamiento topológico

Respuesta: (C)
Explicación: El gráfico no contiene ningún ciclo, por lo que existe un ordenamiento topológico.
P y S deben aparecer antes que R y Q porque hay aristas de P a R y Q, y de S a R y Q.
Consulte Ordenación topológica para obtener más detalles.

4) Sea P un programa QuickSort para ordenar números en orden ascendente usando el primer elemento como pivote. Sean t1 y t2 el número de comparaciones realizadas por P para las entradas {1, 2, 3, 4, 5} y {4, 1, 5, 3, 2} respectivamente. ¿Cuál de los siguientes se cumple?
(A) t1 = 5
(B) t1 < t2
(C) t1 > t2
(D) t1 = t2

Respuesta: (C)
Explicación: cuando se elige el primer elemento o el último elemento como pivote, ocurre el peor de los casos de Quick Sort para las arrays ordenadas.
En cada paso de clasificación rápida, los números se dividen según la siguiente recurrencia.
T(n) = T(n-1) + O(n)

5) Considere la siguiente función C en la que el tamaño es el número de elementos en la array E:
El valor devuelto por la función MyX es el

int MyX(int *E, unsigned int size)
{
    int Y = 0;
    int Z;
    int i, j, k;
  
    for (i = 0; i < size; i++)
        Y = Y + E[i];
  
    for (i = 0; i < size; i++)
        for (j = i; j < size; j++)
        {
            Z = 0;
            for (k = i; k <= j; k++)
                Z = Z + E[k];
            if (Z > Y)
                Y = Z;
        }
    return Y;
}

(A) suma máxima posible de elementos en cualquier subarreglo del arreglo E.
(B) elemento máximo en cualquier subarreglo del arreglo E.
(C) suma de los elementos máximos en todos los subarreglos posibles del arreglo E
(D ) la suma de todos los elementos del arreglo E.

Respuesta: (A)
Explicación: La función que sigue
a Y se usa para almacenar la suma máxima vista hasta ahora y Z se usa para almacenar la suma actual
1) Inicialice Y como suma de todos los elementos
2) Para cada elemento, calcule la suma de todos los subarreglos comenzando con arr[i]. Almacene la suma actual en Z. Si Z es mayor que Y, actualice Y.

Consulte a continuación las soluciones completas de todos los documentos GATE CS 2014
GATE-CS-2014-(Set-1)
GATE-CS-2014-(Set-2)
GATE-CS-2014-(Set-3)

Escriba comentarios si encuentra que alguna de las respuestas/explicaciones es incorrecta, o si desea compartir más información sobre los temas discutidos anteriormente.