Estructuras de datos y algoritmos | Conjunto 34

Se han hecho las siguientes preguntas en el examen GATE CS 2014.

1) Considere el pseudocódigo dado a continuación. La función DoSomething() toma como argumento un puntero a la raíz de un árbol arbitrario representado por la representación LeftMostChild-rightSibling. Cada Node del árbol es de tipo treeNode.

typedef struct treeNode* treeptr;
struct treeNode {
    treeptr leftMostChild, rightSibling;
};
int DoSomething (treeptr tree) {
    int value = 0;
    if (tree != NULL) {
        if (tree->leftMostChild == NULL)
            value = 1;
        else
            value = DoSomething(tree->leftMostChild);
        value = value + DoSomething(tree->rightSibling);
    }
    return(value);
}

Cuando el puntero a la raíz de un árbol se pasa como argumento a HacerAlgo, el valor devuelto por la función corresponde al
(A) número de Nodes internos en el árbol.
(B) altura del árbol.
(C) número de Nodes sin un hermano derecho en el árbol.
(D) número de Nodes hoja en el árbol.

Respuesta: (D)
Lo importante a tener en cuenta en esta pregunta es la representación del árbol. El árbol se representa como el hijo más a la izquierda y el hermano derecho. Entonces, si el hijo más a la izquierda es NULL para un Node, entonces no hay ningún hijo de este Node. Si echamos un vistazo a la función, podemos notar que la función incrementa el «valor» en 1 solo para un Node hoja.

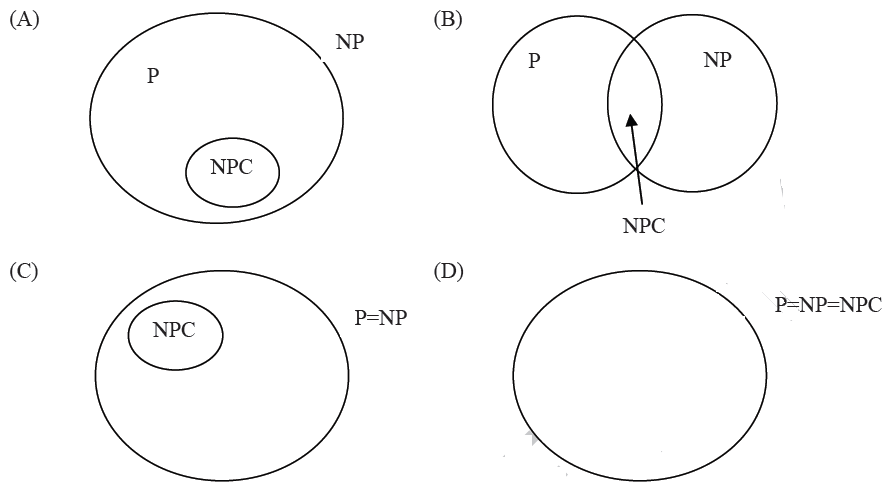
2) Suponga que se descubre un algoritmo de tiempo polinomial que calcula correctamente la camarilla más grande en un gráfico dado. En este escenario, ¿cuál de los siguientes representa el diagrama de Venn correcto de las clases de complejidad P, NP y NP Completa (NPC)?

(A) A
(B) B
(C) C
(D) D

Respuesta: (D)
La camarilla más grande es un problema completo NP. Si un problema NP completo se puede resolver en tiempo polinomial, entonces todos se pueden resolver. Entonces el conjunto de NPC se vuelve igual a P.

Las siguientes son preguntas para llenar los espacios en blanco
3) El número mínimo de comparaciones requeridas para encontrar el mínimo y el máximo de 100 números es _________________.

Respuesta: 147
El número mínimo de comparaciones requeridas es 3n/2 – 3 para n números. Consulte el método 3 de Máximo y mínimo de una array utilizando el número mínimo de comparaciones para obtener más detalles.

4) Considere dos strings A = «qpqrr» y B = «pqprqrp». Sea x la longitud de la subsecuencia común más larga (no necesariamente contigua) entre A y B y sea y el número de tales subsecuencias comunes más largas entre A y B. Entonces x + 10y = ___.

Respuesta: 34
La longitud más larga es 4. Hay 3 LCS de longitud 4 “qprr”, “pqrr” y “qpqr”.

5) Suponga que P, Q, R, S, T son secuencias ordenadas que tienen longitudes de 20, 24, 30, 35, 50 respectivamente. Deben fusionarse en una sola secuencia fusionando dos secuencias a la vez. El número de comparaciones que el algoritmo óptimo necesitará en el peor de los casos para hacer esto es ____.

Respuesta: 358
Para fusionar dos listas de tamaño m y n, necesitamos hacer m+n-1 comparaciones en el peor de los casos. Dado que necesitamos fusionar 2 a la vez, la estrategia óptima sería tomar primero las listas de tamaño más pequeño. La razón para elegir los dos elementos más pequeños es llevar elementos mínimos para la repetición en la fusión.
Primero fusionamos 20 y 24 y obtenemos una lista de 44 usando 43 comparaciones en el peor de los casos. Luego fusionamos 30 y 35 en una lista de 65 usando 64 comparaciones en el peor de los casos. Luego fusionamos 50 y 44 en una lista de 94 usando 93 comparaciones. Finalmente fusionamos 94 y 65 usando 158 comparaciones. Entonces, el número total de comparaciones es 43 + 64 + 93 + 158, que es 358.

Consulte GATE Corner para ver todos los documentos/soluciones/explicaciones del año anterior, plan de estudios, fechas importantes, notas, etc.

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.