Estructuras de datos y algoritmos | Conjunto 35

Se han hecho las siguientes preguntas en el examen GATE CS 2014.

1) El número de árboles de expansión mínimos distintos para el siguiente gráfico ponderado es ____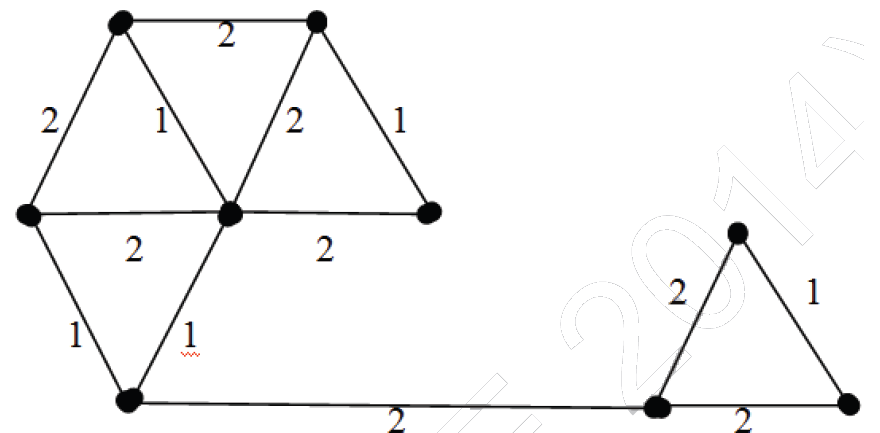

Respuesta: 6
Resaltados (en ) son los bordes elegidos para hacer un MST. En el lado derecho de MST, podríamos elegir el borde ‘a’ o ‘b’. En el lado izquierdo, podríamos elegir ‘c’ o ‘d’ o ‘e’ en MST.
Hay 2 opciones para seleccionar un borde y 3 opciones para seleccionar otro borde. Por lo tanto, sume 2*3 MST posibles.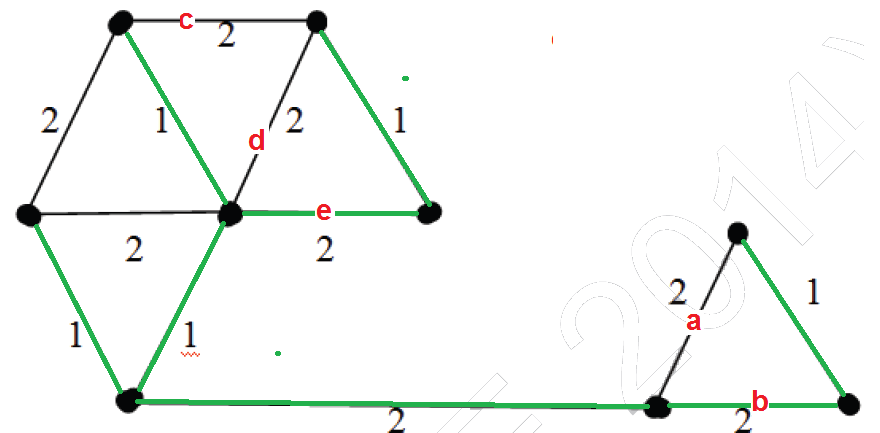

2) Considere el siguiente árbol enraizado con el vértice P etiquetado como raíz. El orden en que se visitan los Nodes durante el recorrido en orden es (A) SQPTRWUV (B) SQPTURWV (C) SQPTWUVR (D) SQPTRUWV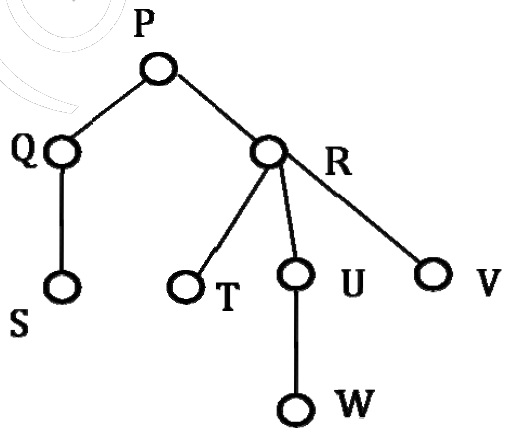

Respuesta: (A)
La única confusión en esta pregunta es que hay 3 hijos de R. Entonces, ¿cuándo debería aparecer R, después de U o después de R? Hay dos posibilidades: SQPTRWUV y SQPTWURV. Solo la primera posibilidad está presente como opción A, la segunda posibilidad no está presente. Por lo tanto, la opción A es la respuesta correcta.

3) Sea A una array cuadrada de tamaño nx n. Considere el siguiente programa. cual es la salida esperada?

C = 100
for i = 1 to n do
    for j = 1 to n do
    {
        Temp = A[i][j] + C
        A[i][j] = A[j][i]
        A[j][i] = Temp - C
    }
for i = 1 to n do
    for j = 1 to n do
        Output(A[i][j]);

(A) La propia array A
(B) Transpuesta de la array A
(C) Sumar 100 a los elementos de la diagonal superior y restar 100 a los elementos de la diagonal de A
(D) Ninguna de las anteriores

Respuesta: A
Si observamos las declaraciones internas de los primeros bucles, podemos notar que las declaraciones intercambian A[i][j] y A[j][i] por todos los i y j.
Dado que el bucle se ejecuta para todos los elementos, cada elemento A[l][m] se intercambiaría dos veces, una vez para i = l y j = my luego para i = m y j = l. Intercambiar dos veces significa que la array no cambia.

4) El número mínimo de operaciones aritméticas requeridas para evaluar el polinomio P(X) = X ⁵ + 4X ³ + 6X + 5 para un valor dado de X usando solo una variable temporal.
(A) 6
(B) 7
(C) 8
(D) 9

Respuesta: B
Podemos poner entre paréntesis el polinomio para minimizar el número de operaciones (Ver Método de Horner ). Obtenemos X(X ² (X ² + 4) + 6) + 5 después del paréntesis.

Following is sequence of operations to be used.
Note that we are allowed to use only one variable.
res = X*X
res = res + 4
res = X*res
res = X*res
res = res + 6
res = X*res
res = res + 5

5) Tienes una array de n elementos. Suponga que implementa la ordenación rápida eligiendo siempre el elemento central de la array como pivote. Entonces, el límite superior más ajustado para el desempeño en el peor de los casos es
(A) O(n ² )
(B) O(nLogn)
(C) Θ(nLogn)
(D) O(n ³ )

Respuesta: (A)
El elemento del medio siempre puede ser un elemento extremo (mínimo o máximo) en orden ordenado, por lo tanto, la complejidad del tiempo en el peor de los casos se convierte en O(n ² )

Consulte GATE Corner para ver todos los artículos/soluciones/explicaciones del año anterior, plan de estudios, fechas importantes, notas, etc.

Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.