Estructuras de datos y algoritmos | Conjunto 36

Que – 1. La función shiftNode() que toma como entrada dos listas vinculadas: destino y origen. Elimina el Node frontal del origen y lo coloca en el frente del destino. Elija el conjunto de declaraciones que reemplazan a X, Y, Z en la función dada.

void shiftNode(struct node** destRoot,
                struct node** srcRoot) 
{
     // the front of source node
     struct node* newNode = *srcRoot;  
     assert(newNode != NULL);
     X;
     Y;    
     Z;
}

(A)

X: *srcRoot = newNode->next
Y: newNode->next = *destRoot->next
Z: *destRoot->next = newNode

(B)

X: *srcRoot->next = newNode->next
Y: newNode->next = *destRoot
Z: *destRoot = newNode->next

(C)

X: *srcRoot = newNode->next
Y: newNode->next = *destRoot
Z: *destRoot = srcRoot->next

(D)

X: *srcRoot = newNode->next
Y: newNode->next = *destRoot
Z: *destRoot = newNode

Solución:
X: mueva el puntero hacia adelante a la lista vinculada de origen.
Y: haga que el nuevo Node apunte al frente de la antigua lista vinculada de destino.
Z: permite que la lista enlazada de destino apunte al nuevo Node.
Entonces, la opción (D) es correcta.
 
Que – 2. Se dice que un vértice v está “terminado” cuando finaliza la recursión DFS(v). ¿Cuál es el orden de los vértices que están «sobre» para el gráfico dado? Considere que el DFS comienza en el vértice a y, en caso de múltiples rutas posibles, viaje en orden alfabético.

(A) efihgcdba
(B) abdcegfhi
(C) abcdegifh
(D) efihdgcba

Solución:
Es importante notar aquí que la respuesta NO es el DFS del gráfico. Los Nodes en rosa dan el orden de DFS. Es decir: abdcegfh i. Los Nodes en verde dan el orden en el que siguen «sobre»: efihgcdb a.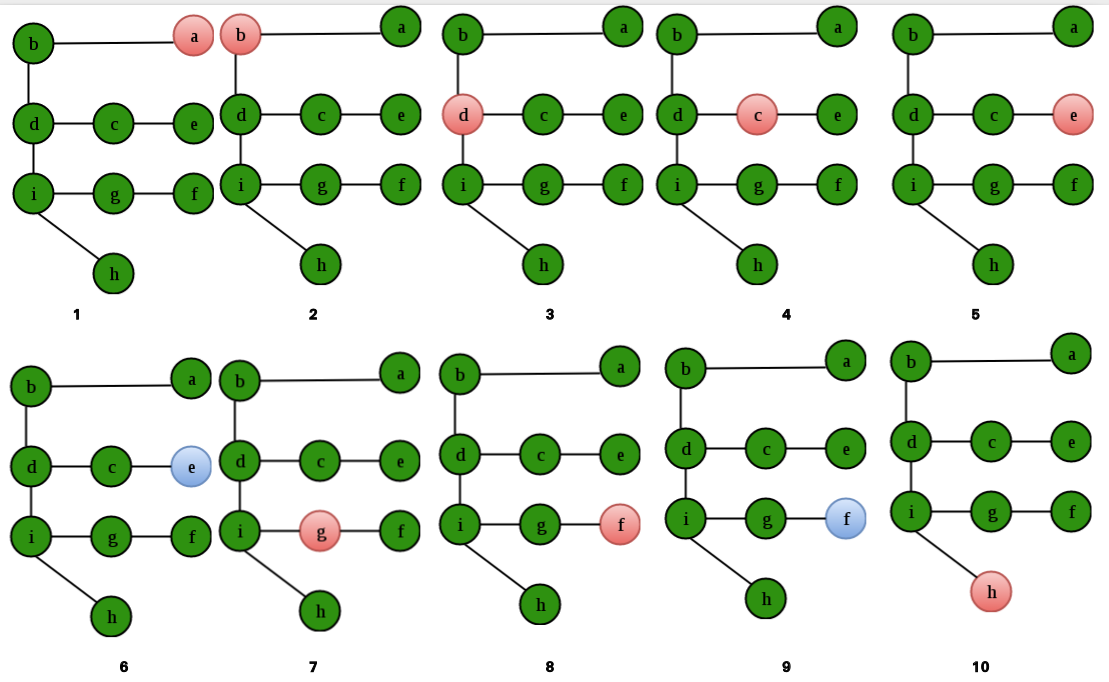


La opción (A) es correcta.

Que – 3. Se le dan dos listas enlazadas individualmente con encabezados head_ref1 y head_ref2 respectivamente. ¿Qué hace la siguiente función?

int myFunc(Node* head_ref1, Node* head_ref2)  {
   Node *pointer1 = head_ref1, *pointer2 = head_ref2;
    while (pointer1 != pointer2)  {
        pointer1 = pointer1?pointer1->next:head_ref2;
        pointer2 = pointer2?pointer2->next:head_ref1;
    }
   return pointer1?pointer1->data:-1;
}

(A) Fusionar las dos listas vinculadas
(B) Encontrar el punto de fusión de las dos listas vinculadas
(C) Intercambiar Nodes de las dos listas vinculadas
(D) El programa se ejecuta en un bucle infinito

Solución:
Los punteros a ambas listas vinculadas continúan incrementándose e intercambiándose entre listas hasta que encuentran un punto común de intersección. La función devuelve -1 si no hay ningún punto de fusión, es decir, cuando puntero1 y puntero2 se encuentran en NULL. Realizar un simulacro en listas enlazadas de muestra aclararía el concepto. 
La opción (B) es correcta.

Que – 4. La función copyBSTNodes() crea una copia de cada Node de un árbol de búsqueda binaria e inserta el Node copiado como el hijo izquierdo del Node original. El árbol resultante sigue siendo un BST. Elija el conjunto de declaraciones que reemplazan a X e Y en la función dada.

void copyBSTNodes (struct node* root)  {
    struct node* prevLeft;
    if (root==NULL) return;

      copyBSTNodes (root->left);
      copyBSTNodes (root->right);
      
      X;
      root->left = newNode(root->data);
      Y;
 }

(A)

X: prevLeft->left = root->left
Y: root->left->left = prevLeft->left

(B)

X: prevLeft = root->left
Y: root->left->left = prevLeft

(C)

X: prevLeft = root
Y: root->left = prevLeft

(d)

X: prevLeft = root->left
Y: root->left->left = prevLeft->left

Solución: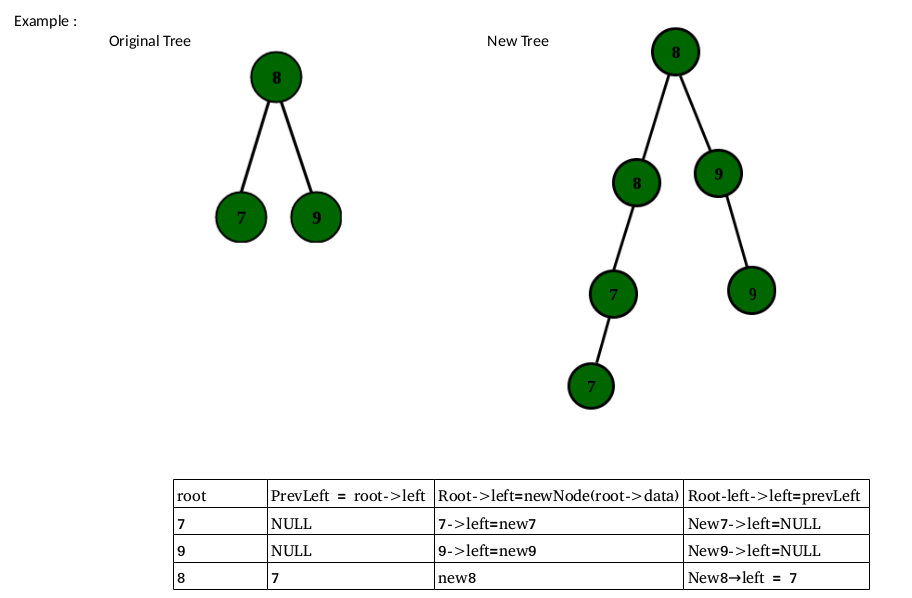

La opción (B) es correcta.

Que – 5. La función eraseDup() toma como entrada una lista enlazada ordenada en orden ascendente. Elimina los Nodes duplicados de la lista atravesándolos solo una vez. Elija el conjunto de declaraciones que reemplazan a X, Y, Z en la función dada.

void eraseDup(struct node* root)  {
    struct node* current = root;
    if (X) 
       return;     

   while (current->next!=NULL)  {
       if (Y)  {
           struct node* nextOfNext = current->next->next;
           free(current->next);
           current->next = nextOfNext;
           }
       else  {
           Z 
          }
     }
 }

(A)

    
X: current == NULL
Y: current = current->next
Z: current->data = current->next->data;

(B)

    
X: current == NULL
Y: current->data == current->next->data
Z: current = current->next;

(C)

X: current->next == NULL
Y: current->next->data == current->next->next->data
Z: current = current->next;

(D)

X: current->next == NULL
Y: current->data = current->next->data
Z: current = current->next;

Solución:
como la lista de enlaces de entrada ya está ordenada, bajamos en la lista mientras comparamos los Nodes uno al lado del otro. Cuando los datos en los Nodes adyacentes son iguales, eliminamos el segundo Node. Nota: El Node que sigue al siguiente debe almacenarse antes de realizar la operación de eliminación.
La opción (B) es correcta.