La ronda 1:
-Te dan unos bloques que descansan en el suelo. Así que tienes una array como: 1, 2, 3, 4 ahora en cada índice que muestra el número de bloques que descansan sobre él. Ahora la dirección de la gravedad cambia de arriba hacia abajo y de derecha a izquierda, cuál será el estado final de los bloques en esta array. Así que el estado final será 4, 3, 2, 1.
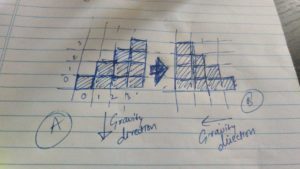
El problema, si se analizaba correctamente, era en realidad un simple problema de clasificación. Hizo algunas preguntas de seguimiento sobre los criterios en los que seleccionamos cualquier algoritmo de clasificación (estable, en el lugar, etc.).
-Se le da una serie de listas vinculadas. Algunas de estas listas son listas enlazadas que se cruzan (tienen Nodes comunes y luego se fusionan en uno). Entonces, por ejemplo, si hay una lista de cuatro Nodes en el índice 0, es posible que haya otra lista en algún otro índice, por ejemplo, el índice 1 cuyos Nodes se fusionan con cualquiera de los Nodes en la lista 0. Así que encuentra el número de grupos conectados en esta estructura. Usé la estructura de datos del conjunto disjunto para resolver este problema.
La ronda 2:
Discusión sobre proyectos
Comprobar si una expresión dada es válida o no. Por ejemplo ((A+B/C)*(DF)) es válido. Y )*A+B) no lo es.
Discusión sobre los formatos de URL de Api y varios verbos de descanso
Discusión sobre varias estrategias de prueba (Unidad, Humo, Integración, automatizaciones de API, etc.).
Ronda 3:
Esta fue una ronda que sube el listón.
P1: Se le da el tamaño de una línea de personas, digamos n y estas n personas pueden pararse en cualquier orden y todas estas n personas tienen alturas distintas. Ahora, desde cualquiera de los extremos de la línea se puede ver decir p y q amigos. Ahora aquí es posible que algunas de las personas de baja estatura estén ocultas detrás de personas más altas.
Para un n, p y q dados, encuentre cuántos arreglos de todas las personas son posibles.
P2: enfoque iterativo y recursivo transversal de preorden
P3: Rompecabezas dados los números (8, 8, 3, 3) necesitas formar 24 usando todos estos números una vez. Puede usar cualquier operador (cubo, raíz cúbica, factorial, +, -, *, /, %)
Además, mientras usa cubo o raíz cúbica, en realidad está consumiendo uno 3.
¡La respuesta fue (raíz cúbica (8) + raíz cúbica (8))!
Q4: permutación de string
P5: hay tres personas en una habitación, digamos P1, P2, P3, todas estas personas tienen algunos salarios, digamos S1, S2 y S3. Ahora bien, ninguna persona está dispuesta a compartir su salario directa o indirectamente de lo que se puede deducir el salario individual. Debe encontrar una manera de encontrar directamente el sol de los salarios de las 3 personas.
La respuesta fue utilizar la asignación al azar. Cada persona generará un número aleatorio y pasará la suma de su salario y el número aleatorio al siguiente. Y así sucesivamente, una vez que tenemos la suma de todos los salarios y los números aleatorios, cada persona puede restar los números aleatorios generados y deducir la suma de los salarios.
P6: Dado un histograma que tiene barras de 1 unidad de ancho y altura variable, encuentre el área máxima de un rectángulo que se puede formar dentro de la barra. (El rectángulo formado debe estar contenido dentro de las barras).
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA