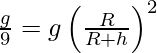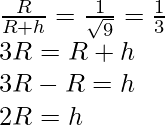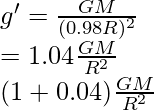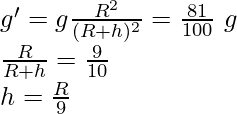Factores que afectan la aceleración debido a la gravedad

Toma algo en tu mano y tíralo al suelo. Su velocidad es cero cuando lo liberas de tu agarre. Su ritmo sube a medida que desciende. Vuela más rápido cuanto más tiempo pasa. Esto suena como aceleración .

La aceleración, por otro lado, implica algo más que aumentar la velocidad. Recoge el mismo objeto y lánzalo al aire verticalmente. Disminuirá la velocidad en el camino hacia arriba hasta que se detenga y cambie de rumbo. La aceleración también puede describirse como una disminución de la velocidad. Sin embargo, la aceleración es más que un simple cambio de altura.

Recoge tu objeto maltratado y dale un último lanzamiento. Esta vez, tírelo horizontalmente y observe cómo aumenta la velocidad horizontal a medida que disminuye la velocidad vertical. Este cambio de dirección a menudo se denomina aceleración, ya que la aceleración es la tasa de cambio de la velocidad con el tiempo y la velocidad es una cantidad vectorial . La aceleración en ambos casos fue causada por la gravedad . Dado que la gravedad estaba arrastrando el objeto hacia abajo, estaba acelerando. Incluso el objeto que está hacia arriba está cayendo, y comienza a caer en el momento en que se aparta de tu lado. Si no lo hubiera sido, habría procedido en línea recta alejándose de ti. Esta es la aceleración de la gravedad.

Ahora, analicemos algunos conceptos básicos antes de comprender los factores que afectan la aceleración debida a la gravedad.

¿Qué es la gravedad?

La fuerza de atracción universal entre todas las entidades o materia en este universo también se conoce como gravedad. Se puede considerar como el motor que aglutina toda la materia. La gravedad se mide en términos de la aceleración o el movimiento que les da a los objetos que caen libremente. En la superficie de la Tierra, el valor de la aceleración de la gravedad es de unos 9,8 m/s ² . Así, por cada segundo que un objeto está en caída libre, su velocidad aumenta en unos 9,8 m/s ² .

Algunos importantes que uno debe aprender antes de continuar son:

Existe una correlación directa entre masa y gravedad, es decir, la masa es directamente proporcional a la gravedad. Cuanto más pesado es el objeto, mayor es la intensidad de la atracción. Por ejemplo, las estrellas y el sol tienen mayor gravedad.

También existe una relación directa entre la masa del objeto y la gravedad, es decir, el aumento de la masa conduce al aumento de la atracción debido a la gravedad.

La gravedad también es inversamente proporcional a la distancia entre dos objetos.

Aceleración debida a la gravedad

La Tierra atrae cualquier partícula que se encuentra en su superficie hacia su centro con una fuerza conocida como atracción gravitacional de la gravedad. Cuando una fuerza actúa sobre un cuerpo, provoca una aceleración, y en el caso de la gravitación, esta aceleración causada por la gravedad se denomina aceleración debida a la gravedad.

La aceleración debida a la gravedad, generalmente referida con el símbolo ‘ g ‘, es la aceleración alcanzada por cualquier objeto en el universo debido a la fuerza gravitatoria.

La unidad SI de aceleración de la gravedad es m/s ² .

El valor de g en el sistema SI es 9.806 ms ^-2 . Y el valor de g en el sistema CGS es 980 cm s ^-2 .

La fórmula dimensional para g es [ M ⁰ L ¹ T ^-2 ] .

Tiene tanto magnitud como dirección. Por lo tanto, es una cantidad vectorial .

Derivación de la fórmula para la Aceleración debida a la Gravedad

Cerca de la superficie de la Tierra, la aceleración de la gravedad es aproximadamente constante. Pero, a grandes distancias de la Tierra, o alrededor de otros planetas o lunas, varía. La aceleración debida a la gravedad depende de los siguientes términos:

masa del cuerpo,
Distancia desde el centro de masa,
Constante G, es decir, constante gravitacional universal.

Consideremos un objeto de masa m, sobre el cual está actuando la aceleración debida a la gravedad g, ahora supongamos que F es la fuerza que actúa sobre él y viene dada por:

F = mg ……(1)

donde F es la fuerza que actúa sobre el objeto,

g es la aceleración de la gravedad y

m es la masa del objeto.

De acuerdo con la ley universal de la gravitación, la fuerza de atracción gravitatoria viene dada por:

F = (G × m × M) / (r+h) ²

donde F es la fuerza entre dos objetos,

G es la constante gravitatoria universal (6,67 × 10 ^-11 Nm ² / kg ² ),

M es la masa de la tierra,

r es el radio de la tierra, y

h es la altura a la que se encuentra el cuerpo desde la superficie de la tierra.

Dado que la altura es insignificantemente pequeña en comparación con el radio de la Tierra, la última ecuación se puede reescribir como:

F = (G × m × M) / r ² ……(2)

Igualemos la ecuación (1) y (2) y resolvamos para evaluar la expresión para g como:

mg = (G × m × M) / r ²

g = GM / r ²

Por lo tanto, la fórmula de la aceleración debida a la gravedad se evalúa como se muestra arriba.

Factores que afectan la aceleración debido a la gravedad

g se ve afectado principalmente por los siguientes cuatro factores:

La forma de la Tierra.
Movimiento de rotación de la Tierra.
Altitud sobre la superficie de la Tierra.
Profundidad debajo de la superficie de la Tierra.

Variación de g debido a la forma de la Tierra

La tierra no es perfectamente esférica, pero es un esferoide achatado. El radio polar (radio cerca de los polos) de la tierra es 21 km más pequeño que su radio ecuatorial (cerca del ecuador). Según la fórmula derivada, la aceleración de la gravedad es inversamente proporcional al cuadrado del radio de la tierra.

$\frac{gp}{ge} = \frac{R^2e}{R^2p}$

Donde, g _e y g _p son las aceleraciones debidas a la gravedad asumidas en el ecuador y los polos, _Re y R _p son los radios de la tierra cerca del ecuador y los polos, respectivamente.

De la ecuación anterior, se puede deducir fácilmente que la aceleración debida a la gravedad es mayor en los polos y menor en el ecuador, es decir, g _e < g _p . Por lo tanto, la aceleración de la gravedad aumenta cuando uno se mueve del ecuador al polo.

Movimiento de rotación de la Tierra.

Supongamos que ω es la velocidad angular de rotación de la tierra sobre su propio eje, entonces la aceleración debida a la gravedad en un lugar que tiene latitud λ se muestra como

g′ = g – Rω² cos² λ

Aquí, λ en los polos es 90° y λ en el ecuador es 0°.

g’ = g

Por lo tanto, no hay efecto de rotación de la tierra sobre su propio eje en los polos.
en el ecuador,

λ = 0° y g’ = g – Rω²
El valor de g es mínimo en el ecuador.
Si la tierra detiene su rotación sobre su propio eje, entonces g permanecerá sin cambios en los polos pero aumentará en Rω² en el ecuador.

Por lo tanto, podemos concluir que;

La aceleración debida a la gravedad es mínima en el ecuador.

En los polos, θ=90°

La aceleración debida a la gravedad es máxima en los polos.

Altitud sobre la superficie de la Tierra

Suponga una masa ‘m’ que está bajo el efecto de la gravedad terrestre a una altura ‘h’ de la superficie terrestre. La fuerza debida al tirón gravitacional que actúa sobre el objeto es;

Aceleración debida a la gravedad a la altura ‘h’ de la superficie terrestre

$F = \frac{GMm}{(R+h)^2}$ ……..(i)

Aquí,

m es la masa de la tierra

R es el radio de la tierra.

La aceleración de la gravedad a cierta altura viene dada por ‘h’

Por lo tanto,

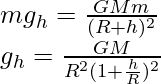$mg_h= \frac{GMm}{(R+h)^2}\\ ⇒ g_h= \frac{GM}{R^2(1+ \frac{h}{R})^2 }$ ……(ii)

Entonces, la aceleración debida a la gravedad en la superficie de la tierra se muestra por;

$g = \frac{GM}{R^2}$ ………..(iii)

Después de dividir la ecuación (iii) y (ii) obtendremos,

$g_h = g (1+\frac{h}{R})^{-2}$ …………(iv)

Está claro que el valor de g disminuye con un aumento en la altura de un objeto. Por lo tanto, el valor de g se vuelve cero a una distancia infinita de la tierra.

Profundidad debajo de la superficie de la Tierra.

La aceleración de la gravedad en la superficie de la tierra está dada por

$g=\frac{GM}{R^2}$

Supongamos $\rho$ que es la densidad del material de la Tierra

Como la conocemos

Masa = volumen × densidad

$M=\frac{4}{3}\pi R^3\rho$ …….(i)

Así, si ponemos el valor de (i) en g, obtendremos

$g=\frac{G}{R^2}\times\frac{4}{3}\pi R^3\times\rho\\ =\frac{4}{3}\pi GR\rho\ \ \ ......(ii)$

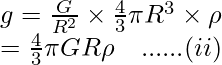
Además, supongamos que se lleva el cuerpo a la profundidad ‘d’ debajo de la superficie de la tierra. Luego, la aceleración debida a la gravedad g _d a la profundidad ‘d’ debajo de la superficie de la Tierra se muestra como;

$g_d=\frac{4}{3}\pi G(R-d)\rho$ ……..(iii)

Ahora, dividiendo la ecuación (iii) por (ii), obtendremos

$\frac{g_d}{g}=\frac{R-d}{R}=1-\frac{d}{R}\\ g_d=g\left(1-\frac{d}{g}\right)\ \ \ ....(iv)$

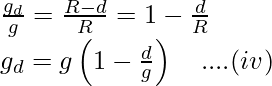
Aquí, la ecuación (iv) es una expresión de la aceleración debida a la gravedad a la profundidad ‘d’ por debajo de la superficie de la tierra.

De la ecuación (iv) sabemos que la aceleración debida a la gravedad disminuye a medida que descendemos hacia la Tierra.

En el centro de la tierra d = R,

Por lo tanto, la aceleración de la gravedad en el centro de la tierra es 0.

Problemas de muestra

Problema 1: ¿A qué altura sobre la superficie de la tierra el valor de la aceleración de la gravedad se reduce a uno por noveno de su valor en la superficie de la tierra?

Solución:

De la fórmula

g _h = $\frac{g}{9}=g\left(\frac{R}{R+h}\right)^2$

Aquí g _h = aceleración de la gravedad a la altura ‘h’

g = aceleración de la gravedad

R = radio de la tierra

De este modo,

del problema

$\frac{R}{R+h}=\frac{1}{\sqrt9}=\frac{1}{3}\\ 3R=R+h\\ 3R-R=h\\ 2R=h$

Por eso,

Al doble de la altura del radio de la Tierra, el valor de la aceleración debida a la gravedad se reduce a uno por noveno de su valor en la superficie de la Tierra.

Problema 2. Si el radio de la Tierra se reduce en un 2% manteniendo su masa igual, ¿cómo cambiará la aceleración de la gravedad?

Solución:

Como sabemos que

$g=\frac{GM}{R^2}$

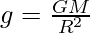
Dónde,

g = aceleración de la gravedad

R = radio de la Tierra

M = masa de la Tierra

Si R se reduce en un 2%, se convertirá en $\frac{98}{100}R$

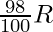
Por lo tanto,

$g'=\frac{GM}{(0.98R)^2}\\ =1.04\frac{GM}{R^2}\\ (1+0.04)\frac{GM}{R^2}$

Por lo tanto,

g’ aumenta en 0,04 por $\frac{GM}{R^2}$ lo tanto aumenta en 4%.

Problema 3. ¿A qué altura de la superficie de la tierra el valor de ‘g’ se reducirá en un 19% de su valor en la superficie de la tierra?

Solución:

g’ = 81% de g

g’ = $\frac{81}{100}\ g$

$g'=g\frac{R^2}{(R+h)^2}=\frac{81}{100}\ g\\ \frac{R}{R+h}=\frac{9}{10}\\ h=\frac{R}{9}$

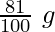
Por lo tanto,

A la altura de $\frac{R}{9}$ la superficie terrestre, el valor de ‘g’ se reducirá al 19% de su valor en la superficie terrestre.

Problema 4. ¿Cuántas veces es la aceleración debida a la gravedad en la superficie de Júpiter en comparación con la superficie de la Tierra?

(Utilice los siguientes datos: m _Tierra = 5,98 × 10 ²⁴ kg, r _Tierra = 6,4 × 10 ⁶ m, m _Júpiter = 1,9 × 10 ²⁷ kg, r _Júpiter = 6,99 × 10 ⁷ m)

Solución:

Para resolver este ejemplo necesitaremos encontrar la razón entre la aceleración debida a la gravedad de Júpiter y la aceleración debida a la gravedad de la Tierra

$\frac{a_g,Jupiter}{a_g,Earth}$

Por la relación;

$a_g=\frac{G_m}{r^2}$

Aquí,

m = masa del planeta

r = radio del planeta

$\frac{a_g,Jupiter}{a_g,earth}=\frac{\frac{Gm_{Jupiter}}{r^2_{jupiter}}}{\frac{Gm_{Earth}}{r^2_{Earth}}}\\ =\frac{Gm_{Jupiter}}{r^2_{Jupiter}}\times\frac{r^2_{Earth}}{Gm_{Earth}}\\ =\frac{m_{Jupiter}r^2_{Earth}}{m_{Earth}r^2_{Jupiter}}\\ =\frac{(1.9\times10^{27}Kg)(6.4\times10^6m)^2}{(5.98\times10^{24}Kg)(6.99\times10^7m)^2}\\ =2.66$

Así, la aceleración debida a la gravedad en la superficie de Júpiter es 2,66 veces mayor que la de la superficie de la Tierra.

Problema 5. Explique la aceleración debida a la gravedad ¿aumenta o disminuye con el aumento de la altitud?

Solución:

Como sabemos que la aceleración de la gravedad a la profundidad de h se muestra como;

$g_h=\left(1-\frac{2h}{R_e}\right)g$

Aquí,

R _e = Radio de la Tierra

g = Aceleración debida a la gravedad en la superficie de la Tierra

Por lo tanto, podemos ver claramente que a partir de la ecuación, la aceleración debida a la gravedad aumenta con la disminución de la altura y disminuye con el aumento de la altura.

Problema 6. Explique que la aceleración de la gravedad es independiente de la masa de la tierra así como de la masa del cuerpo.

Solución:

Como sabemos que la aceleración debida a la gravedad del cuerpo de masa m se muestra como;

$g=\frac{GM}{R^2}$

Aquí,

G = Es la constante gravitacional universal

M = Masa de la Tierra

R = Radio de la Tierra

Así, podemos ver claramente aquí que la aceleración debida a la gravedad es independiente de la masa.

Problema 7. Explique que la aceleración de la gravedad aumenta o disminuye con el aumento de la profundidad.

Solución:

Como sabemos, la aceleración de la gravedad se muestra como;

$g_d=\left(1-\frac{d}{R_e}\right)g$

Por lo tanto, aquí podemos ver claramente que la aceleración de la gravedad aumenta con la disminución de la profundidad y disminuye con el aumento de la profundidad.

Publicación traducida automáticamente

Artículo escrito por yashchuahan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

¿Qué es la gravedad?

Aceleración debida a la gravedad

Derivación de la fórmula para la Aceleración debida a la Gravedad

Factores que afectan la aceleración debido a la gravedad

Problemas de muestra

Deja una respuesta Cancelar la respuesta