La convolución es una operación matemática. Se utiliza en el procesamiento de imágenes en MatLab. Se utiliza una máscara/filtro para convolucionar una imagen con fines de detección de imágenes. Pero MatLab ofrece tres tipos de convolución. Aquí explicaremos la convolución simple.
El filtro se desliza sobre la array de la imagen de izquierda a derecha. Los valores correspondientes de array y filtro se multiplican y se suman. El valor de la array bajo el valor central del filtro se reemplaza por el resultado de la operación de convolución.
Dependiendo de la naturaleza del filtro que se desliza sobre la array, MatLab tenía tres tipos diferentes de convoluciones.
Ejemplo 1:
Given an image matrix:
1st row->[1 2 4]
2nd row->[2 1 3]
3rd row->[3 2 1]
Given filter:
1st row->[1 0 1]
2nd row->[1 0 1]
3rd row->[1 0 1]
Here we are going to apply the 'same' convolution.
The resultant matrix is:[3 10 3]
[5 14 5]
[3 9 3]
misma convolución
Ahora vemos la Misma Convolución. Entonces, en este tipo de convolución, el tamaño de la array resultante es el mismo que el tamaño de la array de entrada. El centro del filtro/máscara se coloca sobre el primer elemento de la primera fila. Luego, el filtro se desliza sobre la array de izquierda a derecha. Una vez que se cubre una fila, el filtro se desliza hacia abajo a la fila siguiente y cambia de lado izquierdo a derecho. La array se rellena con 0 cuando el filtro cuelga fuera de la array.
Nota: El tamaño de la array de salida = el tamaño de la array de entrada.
Ejemplo 1: convolución promedio
Matrix (3, 4): 1st row->[1 5 2 3] 2nd row->[6 7 10 2] 3rd row->[8 4 10 6] Averaging Filter (3, 3): 1st row->[0.1111 0.1111 0.1111] 2nd row->[0.1111 0.1111 0.1111] 3rd row->[0.1111 0.1111 0.1111] Same Convolution result (3, 4): 1st row->[2.1111 3.4444 3.2222 1.8889] 2nd row->[3.4444 5.8889 5.4444 3.6667] 3rd row->[2.7778 5.0000 4.3333 3.1111]
Ejemplo 2: convolución normal
Matrix (3, 4): Row1->[1 5 2 3] Row2->[6 7 10 2] Row3->[8 4 10 6] Normal Filter (3,3): Row1->[1 1 1] Row2->[0 0 0] Row3->[-1 -1 -1] Same Convolution result: Row1->[13 23 19 12] Row2->[6 14 10 11] Row3->[-13 -23 -19 -12]
Tomemos un ejemplo para la Misma convolución y apliquemos la máscara en eso,
Ejemplo:
Matlab
% MATLAB code for Same Convolution % Matrix initialisation; K = [1 5 2 3; 6 7 10 2; 8 4 10 6]; % Averaging mask creation mask1=ones(3,3).*1/9; % Result-1 R1=conv2(K,mask1,'same'); % Random mask mask2=[1 1 1; 0 0 0; -1 -1 -1]; % Result-2 R2=conv2(K,mask2,'same'); % Show matrix-K, mask1 and result-1 K mask1 R1 % Show matrix-K, mask2 and result-2 K mask2 R2
Salida 1:

Salida 2:

Convolución válida
En este tipo de convolución, el tamaño de la array resultante se reduce. El filtro/máscara se coloca sobre la array de tal manera que ninguna parte del filtro sobresalga. El filtro se desplaza completamente sobre la array y luego se desliza de izquierda a derecha en filas y de arriba hacia abajo en columnas.
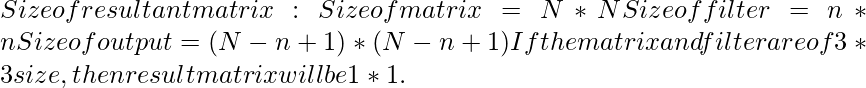
Ejemplo:
Matrix (3, 4): Row 1->[1 5 2 3] Row 2->[6 7 10 2] Row 3->[8 4 10 6] Filter (3,3): Row 1->[1 1 1] Row 2->[0 0 0] Row 3->[-1 -1 -1] Valid Convolution result: [14 10] Number of rows in output matrix = (3 - 3 + 1) = 1 Number of columns in output matrix = (4 - 3 + 1) = 2
Ejemplo:
Matlab
% MATLAB code for % Valid convolution. % Define matrix -1 matrix1 =[1 2 4 3; 2 1 3 5; 3 2 1 6; 2 3 4 9]; % Define mask1 mask1=[1 1 1; 0 0 0; 1 1 1]; % Apply valid convolution. result1=conv2(matrix1,mask1,'valid'); % Show matrix, mask and result. matrix1 mask1 result1 % Define mat-2 matrix2=[1 5 2 3; 6 7 10 2; 8 4 10 6]; % Define mask2 mask2=[1 1 1; 0 0 0; -1 -1 -1]; % Apply valid convolution. result2=conv2(matrix2,mask2,'valid'); % Show matrix, mask and result. matrix2 mask2 result2
Salida 1:

Salida 2:

Convolución completa
En este tipo de convolución,
- La primera parte inferior derecha del filtro se desplazará sobre el elemento superior izquierdo de la array. Se calculará su producto. El resto de los elementos del filtro se multiplicarán por 0 porque la array se rellena con 0 de forma predeterminada. Si estamos usando un filtro promedio, se calculará el promedio del producto.
- La fila inferior del filtro se deslizará sobre la array de izquierda a derecha. La última operación en la primera fila se calculará cuando el elemento más a la izquierda de la fila inferior del filtro pase el cursor sobre el elemento más a la derecha de la primera fila de la array.
- Por lo tanto, después de deslizar la primera fila, el filtro bajará un paso y volverá a repetir los mismos pasos.
- El filtro se deslizará hasta que su primera fila (superior) pase por encima de la última fila (inferior) de la array. Luego se deslizará de izquierda a derecha hasta que el elemento más a la izquierda del filtro se desplace sobre el elemento más a la derecha de la última fila de la array.
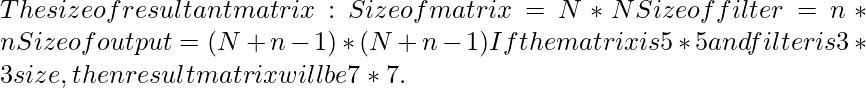
Ejemplo 1:
Input matrix:
1st row->[1 2 4 3]
2nd row->[2 1 3 5]
3rd row->[3 2 1 6]
4th row->[2 3 4 9]
Filter:
1st row->[1 0 1]
2nd row->[0 1 0]
3rd row->[1 0 1]
Resultant matrix:
1st row->[1 2 5 5 4 3]
2nd row->[2 2 7 10 6 5]
3rd row->[4 6 10 16 10 9]
4th row->[4 7 13 19 13 14]
5th row->[3 4 7 12 10 6]
6th row->[2 3 6 12 4 9]
Ejemplo 2:
Matrix (3, 4): [1 5 2 3] [6 7 10 2] [8 4 10 6] Filter (3,3): [1 1 1] [0 0 0] [-1 -1 -1] Full convolution result: [1 6 8 10 5 3] [6 13 23 19 12 2] [7 6 14 10 11 3] [-6 -13 -23 -19 -12 -2] [-8 -12 -22 -20 -16 -6] Rows = (3 + 3 -1) = 5 Columns = (4 + 3 - 1) = 6
Ejemplo:
Matlab
% MATLAB code of % FULL convolution. % Define mat-1 matrix1=[1 2 4 3; 2 1 3 5; 3 2 1 6; 2 3 4 9]; % Define mask1 mask1=[1 0 1; 0 1 0; 1 0 1]; % Apply FULL convolution. result1=conv2(matrix1,mask1,'full'); % Show matrix, mask and result. matrix1 mask1 result1 % Define mat-2 matrix2=[1 5 2 3; 6 7 10 2; 8 4 10 6]; % Define mask2 mask2=[1 1 1; 0 0 0; -1 -1 -1]; % Apply FULL convolution. result2=conv2(matrix2,mask2,'full'); % Show matrix, mask and result. matrix2 mask2 result2
Salida 1:

Salida 2:

Publicación traducida automáticamente
Artículo escrito por pintusaini y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA