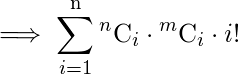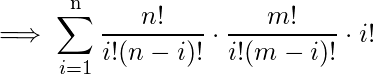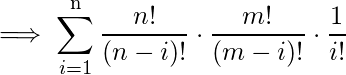Formas de seleccionar uno o más pares de dos conjuntos diferentes

Dados dos números positivos ‘n’ y ‘m’ (n <= m) que representan el número total de elementos del primer y segundo tipo de conjuntos, respectivamente. Encuentre el número total de formas de seleccionar al menos un par seleccionando un artículo del primer tipo (I) y otro artículo del segundo tipo (II). En cualquier arreglo, un artículo no debe ser común entre dos pares.
Nota: Dado que la respuesta puede ser grande, envíela en módulo 1000000007 .

Input: 2 2
Output: 6
Explanation
Let's denote the items of I type
as a, b and II type as c, d i.e,
Type I -  a, b
Type II - c, d
Ways to arrange one pair at a time
1. a --- c
2. a --- d
3. b --- c
4. b --- d
Ways to arrange two pairs at a time
5. a --- c, b --- d
6. a --- d, b --- c

Input: 2 3
Output: 12

Input: 1 2
Output: 2

El enfoque es simple, solo necesitamos la combinación de elegir elementos ‘ i ‘ del tipo ‘ n ‘ y elementos ‘ i ‘ del tipo ‘ m ‘ y multiplicarlos ( Regla del producto ) donde ‘ i ‘ varía de 1 a ‘ n ‘ . Pero también podemos permutar el producto resultante en formas ‘i’, por lo tanto, ¡necesitamos multiplicar con i! . Después de eso, tome la suma ( Regla de la suma ) de todos los productos resultantes para obtener la respuesta final.

// C++ program to find total no. of ways
// to form a pair in two different set
#include <bits/stdc++.h>
using namespace std;
  
// initialize global variable so that
// it can access by preCalculate() and
// nCr() function
int* fact, *inverseMod;
const int mod = 1e9 + 7;
  
/* Iterative Function to calculate (x^y)%p in O(log y) */
int power(int x, int y, int p)
{
    int res = 1; // Initialize result
  
    x = x % p; // Update x if it is more than or
               // equal to p
  
    while (y) {
  
        // If y is odd, multiply x with result
        if (y & 1)
            res = (1LL * res * x) % p;
  
        // y must be even now
        y = y >> 1; // y = y/2
        x = (1LL * x * x) % p;
    } // trace(res);
  
    return res;
}
  
// Pre-calculate factorial and
// Inverse of number
void preCalculate(int n)
{
    fact[0] = inverseMod[0] = 1;
    for (int i = 1; i <= n; ++i) {
  
        fact[i] = (1LL * fact[i - 1] * i) % mod;
        inverseMod[i] = power(fact[i], mod - 2, mod);
    }
}
  
// utility function to calculate nCr
int nPr(int a, int b)
{
    return (1LL * fact[a] * inverseMod[a - b]) % mod;
}
  
int countWays(int n, int m)
{
    fact = new int[m + 1];
    inverseMod = new int[m + 1];
  
    // Pre-calculate factorial and
    // inverse of number
    preCalculate(m);
  
    // Initialize answer
    int ans = 0;
    for (int i = 1; i <= n; ++i) {
  
        ans += (1LL * ((1LL * nPr(n, i) 
                * nPr(m, i)) % mod)
                * inverseMod[i]) % mod;
        if (ans >= mod)
            ans %= mod;
    }
  
    return ans;
}
  
// Driver program
int main()
{
    int n = 2, m = 2;
  
    cout << countWays(n, m);
  
    return 0;
}

// Java program to find total
// no. of ways to form a pair
// in two different set
  
public class Test
{
    static long[] fact;
    static long[] inverseMod;
    static int mod=1000000007;
      
    /* Iterative Function to calculate 
       (x^y)%p in O(log y) */
      
    static long power(long x, int y, int p)
    {
        // Initialize result
        long res = 1; 
      
        // Update x if it is more than or
        // equal to p
        x = x % p; 
      
        while (y!=0)
        {
      
            // If y is odd, multiply 
            // x with result
            if ((y & 1)!=0)
                res = (1 * res * x) % p;
            }
            // y must be even now
            y = y >> 1; 
              
            x = (1 * x * x) % p;
        } 
      
      
        return res;
    }
      
    // Pre-calculate factorial and
    // Inverse of number
    public static void preCalculate(int n)
    {
        //int fact[]=new long[n];
        // int inverseMod[]=new long[n];
        fact[0] = 1;
        inverseMod[0] = 1;
          
        for (int i = 1; i <= n; i++) 
        {
          
                fact[i] = (1 * fact[i - 1] * i)
                                          % mod;
                                            
                inverseMod[i] = power(fact[i], 
                                  mod - 2, mod);
              
        }
    }
      
    // utility function to calculate nCr
    public static long nPr(int a, int b)
    {
          
        return (1 * fact[a] * inverseMod[a - b])
                                    % (long)mod;
    }
          
    public static int countWays(int n, int m)
    {
          
        fact = new long[m + 1];
        inverseMod = new long[m + 1];
          
        // Pre-calculate factorial and
        // inverse of number
        preCalculate(m);
      
        // Initialize answer
        long ans = 0;
          
        for (int i = 1; i <= n; i++) {
      
            ans = ans+(1 * ((1 * nPr(n, i)* 
                                nPr(m, i)) % mod)*
                                (inverseMod[i])) % mod;
                                            
            if (ans >= mod)
                ans %= mod;
        }
      
        return (int)ans;
     } 
      
    /* Driver program */
    public static void main(String[] args) 
    {
        int n = 2, m = 2;
          
        System.out.println(countWays(n, m));
    }
}
  
// This code is contributed by Gitanjali

Producción:

6

Complejidad temporal: O(m*log(mod))
Espacio auxiliar: O(m)

Este artículo es una contribución de Shubham Bansal . Si le gusta GeeksforGeeks y le gustaría contribuir, también puede escribir un artículo usando contribuya.geeksforgeeks.org o envíe su artículo por correo a contribuya@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.