Formas indeterminadas – Barcelona Geeks

Suponga una función $F(x)=\frac{f(x)}{g(x)}$ que no está definida en x=a pero que puede acercarse a un límite cuando x tiende a a. El proceso de determinación de dicho límite se conoce como evaluación de formas indeterminadas. La Regla de L’Hospital ayuda en la evaluación de formas indeterminadas. De acuerdo con esta regla,
$\lim_{x\to a}\frac{f(x)}{g(x)} = \lim_{x\to a}\frac{f'(x)}{g'(x)}$
siempre que tanto f'(x) como g'(x) existan en x = a y g'(x) ≠ 0.

Tipos de formas indeterminadas:

Tipo $\frac{0}{0}$
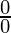
Supongamos que f(x) = 0 = g(x) como x→ a o como x→ 0
Esta forma se puede resolver directamente mediante la aplicación de la regla de L’Hospital.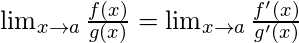
$\lim_{x\to a}\frac{f(x)}{g(x)} = \lim_{x\to a}\frac{f'(x)}{g'(x)}$
Siempre que tanto f'(x) como g'(x) existan en x = a y g'(x) ≠ 0.
Tipo $\frac{\infty}{\infty}$
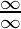
Supongamos que f(x) = ∞ = g(x) como x→ a o como x→ ±∞. Este formulario se puede resolver convirtiéndolo primero al tipo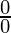 $\frac{0}{0}$ as-
$\frac{f(x)}{g(x)}=\frac{1/g(x)}{1/f(x)}$
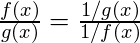
Ahora podemos aplicar la regla de L’Hospital como de costumbre para resolverlo. Se recomienda convertir a la forma 0/0 ya que la diferenciación del numerador y el denominador nunca puede terminar en algunos problemas.
Tipo $0.\infty$
Supongamos que f(x) = 0 y g(x) = ∞ cuando x→ a o x→ ±∞ entonces el producto f(a).g(a) no está definido. Necesitamos resolverlo convirtiéndolo al tipo 0/0 o ∞/∞.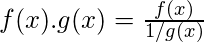
$f(x).g(x)=\frac{f(x)}{1/g(x)}$ o $\frac{g(x)}{1/f(x)}$
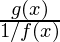
Ahora necesitamos aplicar la regla de L’Hospital.
Tipo $\infty - \infty$
Suponga que f(x) = ∞ = g(x) cuando x→ a. este tipo se resuelve convirtiendo nuevamente a la forma 0/0 mediante el siguiente método: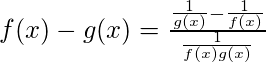
$f(x)-g(x)=\frac{\frac{1}{g(x)}-\frac{1}{f(x)}}{\frac{1}{f(x)g(x)}}$
A medida que logramos la forma 0/0, ahora podemos aplicar la regla L’Hospital.
Tipo $0^0, \infty^0, 1^{\infty}$
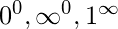
Para evaluar estas formas considere: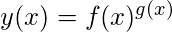
$y(x)=f(x)^{g(x)}$
Tomando el logaritmo de ambos lados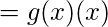
$\lny=g(x)\lnf(x)$
Tomando el límite como x→ a o x→ ±∞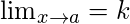
$\lim_{x\to a}\lny=k$
Entonces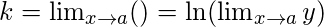 $k=\lim_{x\to a}(\lny)=\ln(\lim_{x\to a}y)$
$=\ln(\lim_{x\to a} f(x)^{g(x)})$
$\lim_{x\to a}f(x)^{g(x)}=e^k$

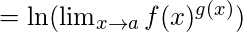
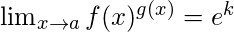
Nota:
si f'(x) y g'(x) no existen en x=a, entonces debemos realizar la diferenciación nuevamente hasta que las derivadas de f(x) y g(x) sean válidas.

Ejemplo-1:
Evaluar $\lim_{x\to 1}\frac{1+\lnx-x}{1-2x+x^2}$

Explicación:
como la función dada asume la forma 0/0 en x = 1, podemos aplicar directamente la regla de L’Hospital.
$F(x)=\frac{f(x)}{g(x)}=\frac{f'(x)}{g'(x)}$
$f(x)=1+\lnx-x \scriptstyle\implies f'(x)=0+1/x-1$
$g(x)=1-2x+x^2 \scriptstyle\implies g'(x)=-2+2x$
Esto forma 0/0 formulario de nuevo. Por lo tanto, aplicamos la regla de L’Hospital nuevamente.
$f''(x)=\frac{-1}{x^2}$ y $g''(x)=2$
así $\lim_{x\to 1} F(x)=\frac{f''(x)}{g''(x)}$
$=\lim_{x \to 1}\frac{-1/x^2}{2}=\frac{-1}{2}$

Ejemplo-2:
Evaluar $\lim_{x\to 1}\log(1-x).\cot\frac{\pi x}{2}$

Explicación:
La función dada asume la forma 0.∞. Primero lo reescribiremos en $\frac{\infty}{\infty}$ forma.
$\lim_{x\to 1}log(1-x).cot\frac{\pi x}{2}=\lim_{x\to 1}\frac{\ln(1-x)}{\tan \pi x/2}$
Ahora aplicamos la regla de L’Hospital para obtener
$\lim_{x\to 1}\frac{1/(1-x).(-1)}{\pi/2.\sec^2 \pi x/2}$
este formulario $\frac{\infty}{\infty}$ nuevamente. Lo reescribimos en forma 0/0 como-
$\lim_{x \to 1}\frac{-2\cos^2\pi x/2}{\pi (1-x)}$
Ahora aplique la regla L’Hospital nuevamente.
$\Lim_{x \to 1}\frac{-2}{\pi}.\frac{2.\cos\pi x/2.(-\sin \pi x/2).\pi/2}{-1}=0$

Publicación traducida automáticamente

Artículo escrito por mohitg593 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta