Un condensador es simplemente un dispositivo eléctrico que consta de dos terminales que tienen la capacidad de almacenar energía en forma de carga eléctrica. Puede diseñarse simplemente colocando dos conductores eléctricos separados entre sí. El espacio vacío entre los conductores se puede llenar con vacío (o aire) o con un material aislante conocido como dieléctrico. La capacidad del capacitor para almacenar cargas se conoce como capacitancia .
En un condensador, los dos terminales que tienen cargas opuestas se colocan a una distancia entre sí que le permite generar (almacenar) energía. El diseño más simple de un condensador es una placa paralela, que consta de dos placas de metal con un espacio entre ellas. Cabe señalar que un capacitor puede tener cualquier forma o tamaño o estar hecho de cualquier material hasta que sus terminales almacenen cargas opuestas y, por lo tanto, almacenen energía.
Capacitancia de un capacitor
Considere un capacitor cuyas placas positiva y negativa tienen carga +q y -q respectivamente. Se aplica una fuente de voltaje de CC a través de él, lo que le da una diferencia de potencial de V a través de las placas. Ahora bien, como sabemos,
Q a V
Poniendo una constante C en esta relación.
Q=CV.
Nota: La capacitancia de cada material es única y su unidad SI es Farad (F).
Funcionamiento de un capacitor
Supongamos que nos dan la forma más básica del condensador, que es un condensador de placas paralelas. Consiste en dos placas paralelas separadas por una pequeña distancia y ese espacio se llena con un dieléctrico. A continuación, se nos proporciona una fuente de voltaje de CC que está conectada a través del capacitor, donde una placa está unida al extremo positivo (placa I) y la otra placa está conectada al extremo negativo (placa II). Cuando el potencial de la batería se aplica a través del capacitor, la placa I se vuelve positiva en relación con la placa II. En estado estacionario, la corriente intenta pasar a través del capacitor desde la placa positiva a la placa negativa. Sin embargo, debido a un espacio entre ellos con una capa aislante (dieléctrica), no puede fluir.

Estructura de un capacitor simple.
Durante algún tiempo, el capacitor continúa cargándose por el flujo de corriente entrante. Pero después de un tiempo llega a un estado en el que tiene la máxima cantidad de carga que puede tener. Así es como un condensador almacena energía. El tiempo que tarda en llegar a este estado de carga máxima se denomina tiempo de carga del condensador. Luego desconectamos la fuente de voltaje del circuito e insertamos una resistencia de carga en él. Ahora la corriente comienza a fluir desde la terminal cargada positivamente del capacitor hacia la terminal cargada negativamente y pierde toda su energía en el proceso. Este período de tiempo se denomina tiempo de descarga del condensador.
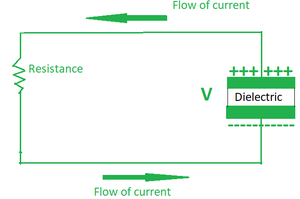
Descarga de un condensador.
Fórmula de capacitor esférico
Como se mencionó anteriormente, la capacitancia ocurre cuando hay una separación entre las dos placas. Entonces, para construir un capacitor esférico, tomamos una esfera hueca de modo que la superficie interna esté cargada positivamente y la superficie externa de la esfera esté cargada negativamente. El radio interior de la esfera es r y el radio exterior viene dado por R. La distancia de Rr entre las dos superficies con carga opuesta actúa como dieléctrico. Supongamos que la superficie esférica interna tiene un potencial de V 1 y V 2.
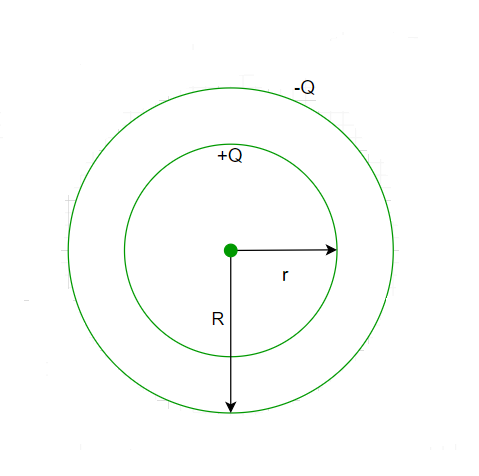
Un condensador esférico
A continuación, el campo eléctrico generado por una esfera cargada (hueca) de radio r con carga Q viene dado por,
E=
. ⇢ (1)
Además, sabemos que el campo eléctrico generado está relacionado con la diferencia de potencial como,
E=
. ⇢ (2)
Comparando (1) y (2),
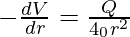
Integrando en ambos lados dentro de los límites V, V y r, R.
⇢ (3)
![]() is the change in potential as we move from inside the sphere to outside. Now the capacitance of a capacitor is given by,
is the change in potential as we move from inside the sphere to outside. Now the capacitance of a capacitor is given by,
⇢ (4)
Comparando (3) y (4),
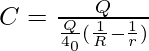
![Rendered by QuickLaTeX.com C = \frac{Q4π∈_0}{Q[\frac{1}{R} - \frac{1}{r}]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-48f9093556ea944d840b58978bfd1a6c_l3.png)
Simplificando aún más obtenemos,
Como la capacitancia no puede ser negativa, se toma el valor positivo. Esta es la expresión de la capacitancia de un capacitor esférico.
Ejemplos de preguntas
Pregunta 1: Un condensador esférico tiene un radio interior de 7 cm y un radio exterior de 10 cm. Encuentre la capacitancia de la esfera. Suponga que el dieléctrico en el medio es aire.
Solución:
La capacitancia de la esfera está dada por,
C =

Aquí ∈ 0 = 8.85 × 10 -12 , r = 7, R = 10
C=
C = 2.593 × 10 -12 F
Pregunta 2: En el problema anterior, encuentre cuánta carga necesitará el capacitor para elevar su potencial de 0 a 10 000 V.
Solución:
La capacitancia del capacitor esférico es C = 2.593 × 10 -12 F.
El cargo requerido se puede encontrar usando Q = CV. donde V es la diferencia de potencial.
La diferencia de potencial V en este caso es 1000-0 = 1000V
Por tanto, Q = 3,7052 × 10 -12 × 1000
Q = 2.593 × 10 -9C
Pregunta 3: El radio interior de un capacitor esférico es xm y su radio exterior es 5/4 xm si el radio exterior aumenta a 3/2x m, encuentre en qué proporción cambia su capacitancia.
Solución:
En este caso
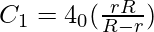
=

= 20 πε o x F
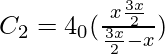
= 20 πε o x F
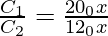
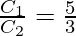
Entonces, la capacitancia disminuye a medida que aumenta el radio externo.
Pregunta 4: Una esfera tiene un radio de 10 cm. encuentre la capacitancia en él y también encuentre la diferencia de potencial requerida para darle una carga de 10^-8 C.
Solución:
C = 4 πε o x F
C = 4 × 3,14 × 8,85 × 10 −12 × 10 × 10 −2
C = 111,156 × 10 −13
C = 1,11 × 10 −11 F
Ahora Q = CV
Por lo tanto
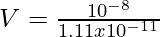
Por lo tanto V = 900,9 V
Pregunta 5: El radio exterior de un condensador esférico es un 10 % más grande que su radio interior. La capacitancia de este capacitor es 10 -8 F. Halle el valor de sus radios interior y exterior.
Responder:
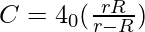
Aquí r = x, R = 1.1x y C= 10 -8 F
Asi que,
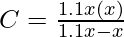

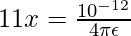
x = 0,009 metros
Por lo que el radio interior es de 0,09 cm y el radio exterior es de 0,099 cm.
Pregunta 6: Los radios interior y exterior de un condensador esférico son 5 cm y 6 cm. Encuentre la energía del capacitor si se le aplica una diferencia de potencial de 1000V.
Solución:
La capacitancia de este capacitor se calcula como,

C = 3,3363 × 10 −12 F
U = 1/2 VC 2
U = 21 × 3.3363 × 10 −12 × (1000) 2
U = 1,66815 × 10 −9 J
Pregunta 7: Un condensador esférico de radios interior y exterior de 8 cm y 10 cm tiene una energía de 10 -8 J . Encuentre su voltaje.
Solución:
Encontremos primero la capacitancia,

C = 4.446 × 10 -9 F
U = 1/2 VC 2
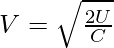
V = 2,12 V
Publicación traducida automáticamente
Artículo escrito por harmansahani100 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA