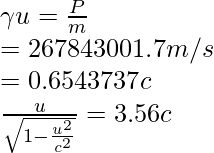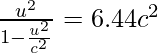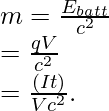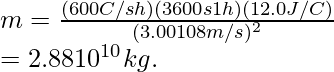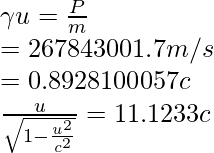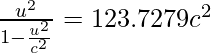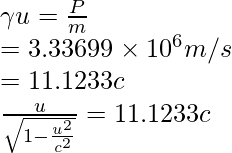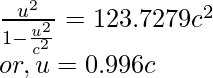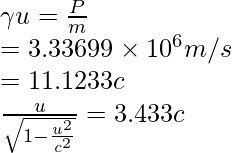La relación energía-momento es una ecuación relativista que se puede usar para vincular la masa, la energía total y el momento de un objeto mientras está en reposo. Esta ecuación relativista se aplica a un cuerpo macroscópico cuya masa en reposo es m 0 , la energía total es E y la magnitud del momento es p, donde c denota la velocidad de la luz como la constante. Esta ecuación se aplica a un sistema con energía total E, masa invariante m 0 y cantidad de movimiento de tamaño p; la constante c es la velocidad de la luz. Tiene en cuenta el escenario de la relatividad especial del espacio-tiempo plano. La energía total es el total del reposo y la energía cinética, mientras que la masa invariable es la masa medida en un marco de centro de masa.
En ambos significados, la relación energía-cantidad de movimiento es congruente con la bien conocida relación masa-energía: E = mc 2 describe la relación entre la energía total E y la masa relativista (total) m (también conocida como mrel o mtot), mientras que E 0 = m 0 c 2 describe la relación entre la energía en reposo E 0 y la masa en reposo (invariable) m 0 .
Fórmula de impulso de energía
La fórmula para la relación energía-momento se da de la siguiente manera,
Dónde,
- E representa la energía.
- p es el momento del objeto.
- c = velocidad de la luz
- m 0 = masa en reposo
Derivación de la fórmula energía-momento
La relación energía-cantidad de movimiento puede derivarse combinando la relación de Einstein con la expresión de la cantidad de movimiento relativista.
E = mc2
p =
⇒
Por lo tanto probado.
Problemas de muestra
Pregunta 1: Encuentra el momento de una partícula de masa 2 × 10 -9 kg con 400 KJ de energía.
Solución:
Dado: E = 400 KJ y m 0 = 2 × 10 -9 kg
La fórmula para la relación energía-momento es
Sustituyendo los valores en la fórmula que tenemos,
p = 119070.4 × 10 8 kg .m/s
Pregunta 2: Encuentra la velocidad de un protón que tiene un momento de 3 × 10 −4 kg⋅m/s.
Solución:
Dado: m = 1,67 × 10 -27 kg y P = 3 × 10 −4 kg⋅m/s
Ya que,
Elevando al cuadrado ambos lados, obtenemos
u = 5,3 × 10 8 m/s
Pregunta 3: A 12,0 V, la batería de un automóvil se evalúa para cambiar 600 amperios-hora (Ah) de carga. Determine el incremento en la masa en reposo de la batería desde completamente descargada hasta recargada, suponiendo que no ocurren reacciones químicas.
Solución:
Dado: E batt = (Δm)c 2
⇒
El tiempo debe convertirse en horas. De este modo,
Pregunta 4: Encuentra la velocidad de un protón que tiene un momento de 4,48 × 10 −19 kg⋅m/s.
Solución:
Dado: m = 1,67 × 10 -27 kg y P = 4,48 × 10 −19 kg⋅m/s
Ya que,
Elevando al cuadrado ambos lados, obtenemos
⇒ u = 0.665996204c
o bien, u = 1,997988 x 10 8 m/s
Pregunta 5: ¿Un objeto con cantidad de movimiento siempre tiene energía? ¿También es cierto lo contrario? Explique.
Solución:
Sí, un objeto con impulso siempre tiene energía. Si el objeto tiene cantidad de movimiento (mv) debe estar en movimiento, y si se está moviendo, tiene energía cinética.
No, un objeto con energía NO siempre tiene impulso. Un objeto puede estar en reposo y tener energía potencial (un libro sobre un escritorio, por ejemplo). Dado que la velocidad de este objeto = 0, su impulso es cero.
Pregunta 6: Encuentra la velocidad de un electrón que tiene un momento de 3,04 × 10 −21 kg⋅m/s.
Solución:
Dado: m = 9,11 × 10 -31 kg y P = 4,48 × 10 −19 kg⋅m/s
Ya que,
Elevando al cuadrado ambos lados, obtenemos
Pregunta 7: Encuentra la velocidad de un electrón que tiene un momento de 5 × 10 −19 kg⋅m/s.
Solución:
Dado: m = 9,11 × 10 -31 kg y P = 5 × 10 −19 kg⋅m/s
Ya que,
Elevando al cuadrado ambos lados, obtenemos:
Publicación traducida automáticamente
Artículo escrito por kamaljeet69420 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

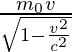
![Rendered by QuickLaTeX.com p^2c^2=\frac{m_0^2v^2c^2}{1-\frac{v^2}{c^2}}\\=\frac{m_0^2\frac{v^2}{c^2}c^4}{1-\frac{v^2}{c^2}}\\= \frac{m_0^2c^4[\frac{v^2}{c^2}-1]}{1-\frac{v^2}{c^2}}+\frac{m_0^2c^4}{1-\frac{v^2}{c^2}} \\=-m_0^2c^4+(mc^2)^2 \\⇒E=\sqrt{p^2c^2+(m_0c^2)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b803e698f6d4c287231bf2b3ee5b98bc_l3.png)