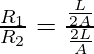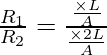Fórmula de resistencia – Part 2

Si uno quiere controlar la corriente que fluye dentro de los cables, entonces necesita saber acerca de la resistencia. En un circuito, es la oposición al flujo de corriente. Se mide en ohmios (Ω). Se puede calcular usando la ley de Ohm. Se define como la relación entre el voltaje aplicado y la corriente. Por lo tanto,

R = V/I

Dónde,

R = resistencia

yo = corriente

V = voltaje

La fórmula de resistencia eléctrica se puede calcular utilizando la longitud y el área de un cable. La fórmula establece que el valor de la resistencia a través de un cable que es directamente proporcional a la longitud e inversamente proporcional al área de la sección transversal.

Matemáticamente, esta relación a menudo se escribe como,

La resistencia del conductor es directamente proporcional a su longitud,

R α L

La resistencia del conductor es inversamente proporcional a su área de sección transversal,

$R α \frac{1}{A}$

Quitando la proporcionalidad y la constante se llama resistividad,

$R = ρ\frac{l}{A}$

Dónde,

R = resistencia

ρ = resistividad del conductor

l = longitud del conductor

A = área de la sección transversal del conductor

La ecuación anterior también se puede escribir como,

$ρ = R\frac{A}{l}$

$l = R\frac{A}{ρ}$

$A = ρ\frac{l}{R}$

La resistencia depende del material del que esté hecho. Los objetos hechos de aislantes eléctricos como el caucho tienden a tener una resistencia muy alta, mientras que los objetos hechos de conductores eléctricos como los metales tienden a tener una resistencia muy baja.

Analogía de la tubería de agua para la resistencia eléctrica

Cuando la longitud de la tubería es larga, la resistencia al flujo de agua será alta.
Cuando el área de la sección transversal de la tubería es alta, la resistencia al flujo de agua es baja.

Relación de la Resistencia Eléctrica con la Potencia

La potencia eléctrica (P) es el producto de la corriente por el voltaje. La unidad SI de potencia es Watt (W). La potencia eléctrica se calcula por la ley de Ohm y por los valores de voltaje, corriente y resistencia.

P = VI

Dónde,

P = Energía Eléctrica

V = Voltaje

Yo = actual

Por la Ley de Ohm sabemos que,

V = IR

Reemplazando el valor de V en la ecuación anterior,

P = Yo ² /R

Cuando se dan los valores de corriente y resistencia, la ecuación es,

P = V ² /R

Efecto de la temperatura sobre la resistencia eléctrica

La resistencia de los materiales cambia por el cambio de temperatura. La cantidad del cambio difiere con los tipos de material.

Rieles

La resistencia eléctrica de los metales puros aumenta cuando aumenta la temperatura. Por lo tanto, los metales tienen un coeficiente de temperatura de resistencia positivo. por ejemplo, cobre, aluminio, plata, etc.

Aleaciones

La resistencia eléctrica de las aleaciones aumenta con el aumento de la temperatura, pero las aleaciones tienen un valor bajo de coeficiente de resistencia de temperatura positivo. por ejemplo, nicromo, etc.

Semiconductores, aislantes y electrolitos

La resistencia eléctrica de los semiconductores y aislantes disminuye con el aumento de la temperatura. Hay disminución en el valor de la resistencia. Por lo tanto, estos materiales tienen un coeficiente de temperatura de resistencia negativo.

Factores que afectan la resistencia eléctrica

Longitud del conductor

Cuanto mayor sea la longitud del cable, más resistencia ofrecerá el cable.

Área de una sección transversal del conductor.

La resistencia del alambre disminuye a medida que aumenta el área de la sección transversal del alambre.

Material del conductor.

Diferentes materiales tienen diferentes resistencias. Para Metales, la resistencia ofrecida es muy baja pero para Aislantes, la resistencia ofrecida es bastante grande.

Temperatura del Material

La resistencia eléctrica de los metales puros y las aleaciones aumenta cuando aumenta la temperatura, pero para los aisladores, la resistencia eléctrica disminuye cuando aumenta la temperatura.

Resistividad

La resistividad eléctrica es una propiedad de un material que es de naturaleza fundamental y mide la fuerza con la que la propiedad resiste la corriente eléctrica. La unidad SI de resistividad eléctrica es ohmios metro y el símbolo es fila (ρ).

Para casos ideales, donde la sección transversal y la composición física del material son uniformes en toda la muestra. La resistividad se puede escribir como:

$ρ = R\frac{A}{l}$

Para casos menos ideales, la corriente y el campo eléctrico varían en diferentes partes del material. Usamos una expresión general,

$ρ= \frac{E}{J}$

Dónde,

ρ es que la resistencia eléctrica del metal Ω.m

E es que el campo eléctrico en Vm ^-1

J es que la densidad de corriente en Am-2

Problemas de muestra

Pregunta 1: ¿Qué es la ley de Ohm?

Responder:

La ley de Ohm establece que la corriente a través de un conductor entre dos puntos es directamente proporcional al voltaje a través de los dos puntos.

Pregunta 2: Dos alambres de 50m y 40m de longitud respectivamente tienen la misma área de sección transversal y están hechos del mismo material. ¿Qué alambre tiene mayor resistencia?

Responder:

Sabemos que R α L, el cable de 50 m de longitud ofrecerá mayor resistencia. La resistencia de un cable pequeño es baja mientras que la resistencia de un cable largo es alta. t

Pregunta 3: Dos cables L1 y L2 tienen longitudes L y 2L respectivamente. El área de la sección transversal es 2A y A respectivamente. Ambos cables están hechos del mismo material. Encuentre la relación de resistencia en el cable L ₁ y L ₂ ?

Solución:

$R = ρ\frac{l}{A}$

Asi que,

$R_1 = ρ\frac{L}{2A}$ ⇢ (1)

$R_2 = ρ\frac{2L}{A}$ ⇢ (2)

Dividiendo la ecuación 1 por la ecuación 2 sobre dos ecuaciones,

$\frac{R_1}{R_2} = \frac{ρ\frac{L}{2A}}{ρ\frac{2L}{A}}$

$\frac{R_1}{R_2} = \frac{1}{4}$

Pregunta 4: Calcule la resistencia de un alambre de cobre de 5 m de longitud y un área de sección transversal de 2 × 10 ^-6 m². La resistividad del cobre es 1,7 × 10 ^-8 Ωm.

Solución:

Longitud del alambre de cobre = 5m

Área de sección transversal del alambre de cobre = 2 $\times$ 10 ^-6 m ²

Resistividad del alambre de cobre = 1,7 × 10 ^-8 Ωm

Lo sabemos,

$R = ρ\frac{l}{A}$

Entonces, poniendo los valores de ρ, l y A en la ecuación anterior,

$R = \frac{(1.7 \times 10^{-6})\times (5)}{2 \times 10^{-6}}$

R = 4,25 × 10 ^-2 Ω

Pregunta 5: ¿Qué es la resistividad?

Responder:

La resistividad eléctrica es una propiedad fundamental de un material que mide qué tan fuerte resiste la corriente eléctrica. La unidad SI de resistividad eléctrica es el ohmímetro y el símbolo es la fila (ρ).

Pregunta 6: Explique la relación de Potencia con Resistencia?

Responder:

La potencia es voltaje por corriente,

P = VI ⇢ (1)

De la Ley de Ohm,

V = IR ⇢ (2)

Reemplazando el valor de la ecuación (2) en la ecuación (1),

P = yo ² R

También se puede reescribir como,

$P = \frac{V^2}{R}$

Pregunta 7: ¿Qué corriente tomará un aparato de 1500W si la tensión de alimentación es de 220V?

Solución:

Potencia del aparato = 1500W

Tensión de alimentación del aparato = 220V

De la relación potencia-corriente sabemos que,

P = VI

La ecuación anterior se puede reescribir como,

$I = \frac{P}{V}$

$I = \frac{1500}{220}$

Yo = 6.81A

Pregunta 8: Calcula la corriente y la resistencia de un foco eléctrico de 50W,100V.

Solución:

Potencia del aparato = 100W

Voltaje = 100V

De la relación potencia-corriente sabemos que,

P = VI

También,

$I = \frac{P}{V}$

$I = \frac{50}{100}$

Yo = 0.5A

Entonces, la corriente = 0.5A

De la Ley de Ohm,

$R = \frac{V}{I}$

$R = \frac{100}{0.5}$

R = 200Ω

La Resistencia que ofrece la Bombilla Eléctrica = 200Ω

Pregunta 9: ¿Qué sucede con la resistencia de los aisladores con un aumento de temperatura?

Responder:

Con un aumento de temperatura, la resistencia de los aisladores disminuye. Por lo tanto, dicho material tiene un coeficiente de temperatura de resistencia negativo.

Pregunta 10: Un alambre de metal de resistividad 6 × 10 ^-6 Ωm y longitud 20m tiene una resistencia de 10Ω. Calcula su radio.

Responder:

Resistividad del alambre = 6 × 10 ^-6 Ωm

Longitud del cable = 20m

Resistencia del alambre = 10Ω

$R = ρ\frac{l}{A}$

La ecuación anterior se puede reescribir como,

$A = ρ\frac{l}{R}$ ⇢ (1)

Reemplazando los valores en la ecuación (1),

$A = \frac{(6\times 10^{-6})\times (20)}{10}$

A = 12 × 10 ^-6 m ² ⇢ (2)

Generalmente, la sección transversal del área de un cable es un círculo. Entonces el área de un círculo es,

A = πr ² ⇢ (3)

r = radio de la sección transversal del alambre

Poniendo el valor de (2) en (3),

πr2 ⁼ 12 × 10 ^-6

r = 1,954 × 10 ^-3 m

Pregunta 11: Inicialmente, la longitud del cable es L. La longitud del cable se cambia de L a 2L manteniendo igual el área de la sección transversal. ¿Encuentra la relación inicial a final de resistencia?

Solución:

Inicialmente,

La longitud del cable = Lm

El área de la sección transversal del cable = Am ²

Resistencia del cable = R2Ω

Finalmente,

La longitud del cable = 2Lm

El área de la sección transversal del cable = Am ²

Resistencia del cable = R2Ω

La razón de inicial a final es,

$\frac{R_1}{R_2} = \frac{\frac{ρ\times L}{A}}{\frac{ρ\times 2L}{A}}$

$\frac{R_1}{R_2} = \frac{1}{2}$

Pregunta 12: ¿Cuál es la unidad SI de resistividad?

Responder:

La unidad SI de resistividad es la fila (ρ).

Publicación traducida automáticamente

Artículo escrito por gautamgoel962 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Relación de la Resistencia Eléctrica con la Potencia

Efecto de la temperatura sobre la resistencia eléctrica

Resistividad

Problemas de muestra

Deja una respuesta Cancelar la respuesta