La velocidad angular promedio se define como la relación entre el desplazamiento angular y el tiempo que tarda el objeto en sufrir el desplazamiento. Se denota por ω av .
ω av = desplazamiento angular / viaje en el tiempo
Considere el movimiento de una partícula en una trayectoria circular con centro en O.
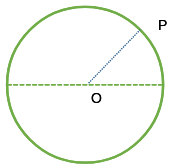
Supongamos que en el tiempo Δt la partícula se desplaza un ángulo de Δθ .
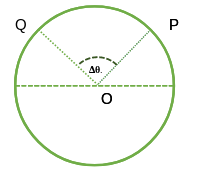
entonces la velocidad angular promedio ω av = Δθ/ Δt
Dado que Δθ es escalar, la velocidad angular promedio es una cantidad escalar.
Velocidad angular instantánea
Es el valor límite de la velocidad angular media del objeto en un pequeño intervalo de tiempo, a medida que el intervalo de tiempo se aproxima a cero. Se denota por ω.
ω = Lt t -> 0 Δθ/ Δt = dθ/dt
La velocidad angular se mide en radianes por segundo y su unidad es rad/s.
Como dθ es un vector, ω también es un vector.
Relación entre velocidad angular y velocidad lineal.
La velocidad lineal es el producto cruzado de la velocidad angular y el radio de la trayectoria circular.
v = ωxr
dónde,
v = velocidad lineal,
ω = velocidad angular &
r = vector de posición desde el centro de la trayectoria circular (radio).
Los términos período de tiempo y frecuencia son sinónimos de velocidad angular, por lo que es necesario definirlos junto con la velocidad angular.
Periodo de tiempo
El tiempo que se tarda en completar una revolución o en desplazarse un ángulo de 2π radianes se denomina período de tiempo y se denota por T .
como la velocidad angular ω es igual al desplazamiento angular/tiempo, por lo tanto, el período de tiempo está relacionado con la velocidad angular como
ω = 2π/ T
T = 2π/ω
Frecuencia
La frecuencia de un objeto es el número de revoluciones completadas en un segundo. Se denota con la letra griega nu ( ν ).
v = 1/T = ω/2π
Problemas de muestra
Problema 1: Calcular la velocidad angular del minutero de un reloj.
El minutero completa una rotación en 60 minutos.
=> se desplaza 2π radianes en 60*60 segundos
=> ω = 2π/3600 = 1,74 * 10 -3 rad/seg.
Problema 2: Una pelota gira en un círculo de 4 m de diámetro con una velocidad de 20 m/s, encuentre su velocidad angular.
radio del círculo = diámetro/2 = 4/2 = 2m
velocidad lineal = 20 m/s
velocidad angular = v / r
ω = 20 / 2 = 10 rad/s
Problema 3: Un objeto gira en un círculo horizontal de radio 12 m con una frecuencia de 4 hz. Encuentre su velocidad lineal.
Velocidad lineal v = ω * r
frecuencia (f) = ω/2π
=> ω = 2π * f
=> v = 2π * f * r
=> v = 301,59 m/s.
Problema 4: Un objeto tiene una velocidad angular constante de 5 rad/s. ¿Cuál es su desplazamiento angular en radianes después de 12 segundos?
Velocidad angular = desplazamiento angular/tiempo
=> desplazamiento angular = velocidad angular * tiempo
=> desplazamiento angular = 5 * 12 = 60 radianes.
Publicación traducida automáticamente
Artículo escrito por harshupadhayay906 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA