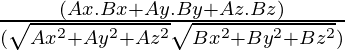Una cantidad vectorial son aquellas cantidades físicas que tienen tanto magnitud como dirección. Cuando dos vectores actúan sobre una partícula, la acción resultante sobre la partícula dependerá del ángulo entre esos vectores. Por lo tanto, es importante conocer el ángulo entre ellos.
Algunas propiedades del Vector para el cálculo de ángulos
Un vector está representado por una flecha paralela a la dirección del vector.
- Un vector permanece sin cambios si se transmite paralelo a sí mismo.
- Dos vectores que tienen la misma dirección son vectores paralelos.
- Dos vectores que tienen direcciones opuestas son vectores antiparalelos.
- Dos vectores que tienen la misma magnitud y dirección son vectores iguales.
- Dos vectores que tienen la misma magnitud y la dirección opuesta se llaman vectores negativos.
Producto escalar
También se conoce como el producto escalar de vectores. Sólo tiene magnitud pero no dirección.

Dos vectores A y B
Entonces el producto punto de A y B está dado por,
![]() = |A| |B| cosθ.
= |A| |B| cosθ.
Casos especiales
- Cuando el ángulo entre los vectores es de 0 grados.
Eso es θ = 0°
⇒ |A| |B| cosθ.
⇒ |A| |B| cos0°
⇒ |A| |B| [cos0° = 1]
- Cuando el ángulo entre los vectores es de 180 grados.
⇒ |A| |B| cosθ.
⇒ |A| |B| cos180°
⇒ – |A| |B| [cos180° = -1]
- Cuando el ángulo entre los vectores es de 90 grados.
⇒ |A| |B| cosθ.
⇒ |A| |B| cos90°
⇒ |A| |B| × 0 [cos90° = 0]
⇒ 0.
Fórmula para el ángulo entre dos vectores
El coseno del ángulo entre dos vectores es igual a la suma del producto de los constituyentes individuales de los dos vectores, dividida por el producto de la magnitud de los dos vectores.

Dos vectores A y B
=| un | | B | cosθ.
cosθ=
θ= cos -1
En forma cartesiana,
A = A x yo + A y j + A z k
segundo = segundo x yo + segundo y j + segundo z k
cosθ =
Propiedades del producto punto
- El producto escalar es conmutativo.
- El producto punto es distributivo.
En física por convección, el ángulo entre dos vectores se encuentra entre 0 ≤ θ ≤ 180. Cuando las colas o cabezas de ambos vectores coinciden, entonces se calcula el ángulo entre vectores.

Coincidencia de cola

cabeza coincidente
Problemas de muestra
Pregunta 1: Encuentra el ángulo entre vectores (si forman un triángulo equilátero)
- Vectores de a y b
- Vectores de b y c
- Vectores de a y c

Triángulo equilátero formado por un vector a, b, c
Solución:
- Vectores de a y b
Para el vector a y b, la cabeza de ambos vectores coincide entre sí, por lo tanto, el ángulo entre el vector a y b es el mismo que el ángulo entre dos lados del triángulo equilátero = 60 °.
- vectores b y c:
De la figura anterior, vemos que la cabeza o la cola del vector b y c no coinciden entre sí.
Entonces, al usar la propiedad: un vector permanece sin cambios si se transmite paralelo a sí mismo.

El vector c se desplaza paralelo a sí mismo.
Ahora vemos que las colas de los vectores b y c son coincidentes entre sí, por lo tanto es lo mismo que el ángulo exterior formado con un triángulo equilátero = 120°.
- Vectores de a y c

La cola de a y c coinciden
Para los vectores a y c, la cola de ambos vectores coincide entre sí, por lo tanto, el ángulo entre el vector a y c es el mismo que el ángulo entre dos lados del triángulo equilátero = 60 °.
Pregunta 2: Encuentra ángulos entre vectores si forman un triángulo rectángulo isósceles.
- vector a y b
- vectores b y c
- Vectores de a y c
Solución:
- vector a y b

Triángulo isósceles de ángulo recto
De la figura anterior, vemos que la cabeza o la cola de los vectores a y b no coinciden entre sí. Entonces, al usar la propiedad: un vector permanece sin cambios si se transmite paralelo a sí mismo.

un vector se desplaza paralelo a si mismo
Ahora, las colas de los vectores a y b coinciden entre sí y forman un ángulo igual al ángulo exterior de un triángulo isósceles de ángulo recto = 135°.
- vectores b y c

Triángulo isósceles de ángulo recto
De la figura anterior, la cabeza o la cola de los vectores b y c no coinciden entre sí. Entonces, al usar la propiedad, un vector permanece sin cambios si se transmite paralelo a sí mismo.

b vector se desplaza paralelo a sí mismo
Ahora, las colas de los vectores b y c coinciden entre sí y forman un ángulo igual al ángulo exterior de un triángulo isósceles de ángulo recto = 135°.
- Vectores de a y c

Triángulo isósceles de ángulo recto
De la figura anterior, las cabezas o colas de los vectores a y c no coinciden entre sí. Entonces, al usar la propiedad: un vector permanece sin cambios si se transmite paralelo a sí mismo.

el vector c se mueve paralelo a si mismo
Ahora, las colas de los vectores a y c coinciden entre sí y forman un ángulo igual al ángulo recto del triángulo isósceles = 90°.
Pregunta 3: Encuentra el ángulo entre los vectores A = i + j + k y el vector B = -2i – 2j – 2k.
Solución:
De la fórmula,
A = A x yo + A y j + A z k
segundo = segundo x yo + segundo y j + segundo z k
cosθ=
Aquí en la pregunta dada,
A = yo + j + k.
B= -2i -2j -2k.
Sustituyendo los valores en la fórmula
⇒ cosθ =
⇒ cosθ =
⇒ cosθ =
⇒ cosθ =
⇒ cosθ = -6/6
⇒ cosθ= -1
⇒ θ = 180°.
Pregunta 4: Encuentra el ángulo entre el vector A = 3i + 4j y B = 2i + j
Solución:
A = A x yo + A y j + A z k
segundo = segundo x yo + segundo y j + segundo z k
cosθ =
Aquí dado,
A= 3i + 4j + 0k
B= 2i + j + 0k
Sustituyendo los valores en la fórmula,
⇒ cosθ =
⇒ cosθ =
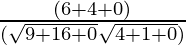
⇒ cosθ =
⇒ cosθ =
⇒ θ = cos -1 (
)
⇒ θ = cos -1 (
)
Pregunta 5: Encuentra el ángulo entre el vector A = i + j y el vector B = j + k.
Solución:
De la fórmula,
A = A x yo + A y j + A z k
segundo = segundo x yo + segundo y j + segundo z k
cosθ =

Aquí en la pregunta dada,
⇒ A = yo + j
⇒ segundo = j + k
⇒ cosθ =
⇒ cosθ =
⇒ cosθ =
.
⇒ θ = cos -1 (1/2)
⇒ θ = 60°.
Publicación traducida automáticamente
Artículo escrito por guptavivek0503 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA