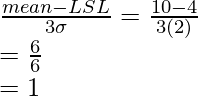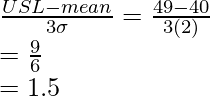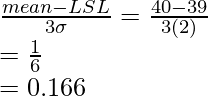Fórmula del índice de capacidad del proceso (Cpk)

La capacidad del proceso (Cp) es un enfoque para determinar el atributo cuantificable de un proceso en relación con una especificación. El índice de capacidad del proceso se abrevia como Cpk (Cpk). Evalúa la capacidad de un fabricante para crear un producto dentro del rango de tolerancia de un cliente. El Cpk se usa para determinar qué tan cerca está de lograr una meta y qué tan consistente es su desempeño en comparación con su promedio. Cpk calcula el mejor de los casos para su procedimiento actual.

Índice de capacidad de proceso

Cpk es un índice de capacidad de proceso que determina cuánto puede producir un proceso. Cpk, a diferencia de Cp, no asume que la media del proceso está centrada entre los límites especificados. Mucha gente usa la capacidad de proceso como una herramienta de cálculo para estimar el resultado de un producto que están fabricando. Ayuda a los fabricantes a estimar la producción potencial y gestionar los recursos para obtener los mejores resultados. El análisis estadístico típico y la distribución de los datos recopilados se utilizan con frecuencia como entradas para el índice de capacidad del proceso. Es análogo a los términos matemáticos media y valor promedio, así como a la desviación estándar. Sin embargo, varía en que emplea un análisis gráfico de control para evaluar el control estadístico del sistema.

Cpk requiere la suposición de que las mediciones se distribuyen regularmente. 

Fórmula

dónde,

• σ es la desviación estándar.
• límite de especificación superior = USL
• límite de especificación inferior = LSL

Interpretación de los valores de CpK

• Si el valor de Cp es igual al valor de Cpk, el proceso está funcionando en el borde. La capacidad de producción es adecuada y cumple con los parámetros de diseño para los estándares Six Sigma.
• La media del proceso ha violado uno de los límites de especificación si Cpk es menor que cero.
• Cuando Cpk es mayor que cero pero menor que uno, la media del proceso está dentro de las limitaciones de especificación, pero una parte de la producción de fabricación las ha excedido.
• La media del proceso está correctamente centrada y dentro de los límites de especificación si Cpk es mayor que uno.

Problemas de muestra

Pregunta 1. La temperatura de una habitación en un hospital donde descansa un paciente debe estar entre 4°C y 20°C. Si la temperatura media es 10 y la desviación estándar es 2, encuentre el índice de capacidad del proceso.

Solución:

Dado: USL = 20°C, LSL = 4°C, Media = 10 y σ = 2°C

Sabemos, 

⇒ 

⇒ 

⇒ Cpk = min (1.667, 1)

Dado que 1 es el valor mínimo de las dos cantidades, el índice de capacidad del proceso es 1.

Pregunta 2. Cuando se le da comida a un cliente en un restaurante, debe estar entre 39°C y 49°C. El procedimiento utilizado para mantener el alimento a la temperatura adecuada tiene una variación estándar de proceso de 2°C, con una temperatura media de 40. ¿Cuál es el índice de capacidad de proceso del proceso?

Solución:

Dado: USL = 49°C, LSL = 39°C, Media = 40 y σ = 2°C

Sabemos, 

⇒ 

⇒ 

⇒ Cpk = mín. (1,5, 0,166)

Dado que 0,166 es el valor mínimo de las dos cantidades, el índice de capacidad del proceso es 0,166.

Pregunta 3. El tiempo dedicado a una tarea debe estar entre 0 horas y 18 horas. Si el tiempo medio es 10 y la desviación estándar es 2, encuentre el índice de capacidad del proceso.

Solución:

Dado: USL = 18, LSL = 0, Media = 10 y σ = 2°C

Sabemos, 

⇒ 

⇒ 

⇒ Cpk = min (1.33, 1.67)

Dado que 1,33 es el valor mínimo de las dos cantidades, el índice de capacidad del proceso es 1,33.

Pregunta 4. ¿Qué implica un valor de Cpk de 1,33 o más?

Solución:

Cpk es un índice estándar para indicar la capacidad de un proceso, cuanto mayor sea el valor de Cpk, mejor será el proceso. Por ejemplo, la Máquina 1 tiene un Cpk de 1,7 y la máquina 2 tiene un Cpk de 1,1. A partir del valor de Cpk, se puede deducir que la Máquina 1 es mejor que la 2.

Cpk = o >1.33 indica que el proceso es capaz y cumple con los límites de especificación. Cualquier valor inferior a este puede significar que la variación es demasiado amplia en comparación con la especificación o que el promedio del proceso se aleja del objetivo.

Pregunta 5. Dado que la media = 10 cm, las especificaciones = 5 – 13 cm. Además, límite de especificación superior = μ + 1σ y límite de especificación inferior = μ – 1σ. Calcule la desviación estándar y el índice de capacidad del proceso.

Solución:

Dado: USL = μ + 1σ = 13 y 

LSL = μ – 1σ = 5

Restando el LSL del USL, tenemos:

2σ = 8 cm

⇒ σ = 4 cm

Sabemos, 

⇒ 

⇒ Cpk = min (0,25, 0,41)

Dado que 0,25 es el valor mínimo de las dos cantidades, el índice de capacidad del proceso es 0,25.