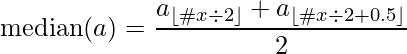función mediana() en el módulo de estadísticas de Python

Python es un lenguaje muy popular cuando se trata de análisis de datos y estadísticas. Afortunadamente, Python3 proporciona un módulo de estadísticas, que viene con funciones muy útiles como mean(), mediana(), mode(), etc. La función
mediana() en el módulo de estadísticas se puede usar para calcular el valor medio de una lista de datos desordenada. La mayor ventaja de usar la función mediana() es que no es necesario ordenar la lista de datos antes de enviarla como parámetro a la función mediana().
La mediana es el valor que separa la mitad superior de una muestra de datos o distribución de probabilidad de la mitad inferior. Para un conjunto de datos, puede considerarse como el valor medio. La mediana es la medida de la tendencia central de las propiedades de un conjunto de datos en estadística y teoría de la probabilidad. La mediana tiene una ventaja muy grande sobre la media, que es que el valor de la mediana no está tan sesgado por valores extremadamente grandes o pequeños. El valor medio está contenido en el conjunto de datos de valores proporcionados o no se desvía demasiado de los datos proporcionados.
Para un conjunto impar de elementos, el valor de la mediana es el del medio. 
Para un conjunto par de elementos, el valor de la mediana es la media de dos elementos intermedios.
 

Median can be represented by the following formula :

Sintaxis: mediana ( [conjunto de datos] )
Parámetros:  
[conjunto de datos] : lista o tupla o un iterable con un conjunto de valores numéricos
Devuelve: devuelve la mediana (valor medio) del iterable que contiene los datos
Excepciones: se genera un error estadístico cuando iterable pasado está vacío o cuando la lista es nula. 
 

Código #1: Trabajando
 

# Python code to demonstrate the 
# working of median() function.
 
# importing statistics module
import statistics
 
# unsorted list of random integers
data1 = [2, -2, 3, 6, 9, 4, 5, -1]
 
 
# Printing median of the
# random data-set
print("Median of data-set is : % s "
        % (statistics.median(data1)))

Producción : 
 

Median of data-set is : 3.5 

  
Código #2: 
 

# Python code to demonstrate the
# working of median() on various
# range of data-sets
 
# importing the statistics module
from statistics import median
 
# Importing fractions module as fr
from fractions import Fraction as fr
 
# tuple of positive integer numbers
data1 = (2, 3, 4, 5, 7, 9, 11)
 
# tuple of floating point values
data2 = (2.4, 5.1, 6.7, 8.9)
 
# tuple of fractional numbers
data3 = (fr(1, 2), fr(44, 12),
         fr(10, 3), fr(2, 3))
 
# tuple of a set of  negative integers
data4 = (-5, -1, -12, -19, -3)
 
# tuple of set of positive
# and negative integers
data5 = (-1, -2, -3, -4, 4, 3, 2, 1)
 
# Printing the median of above datasets
print("Median of data-set 1 is % s" % (median(data1)))
print("Median of data-set 2 is % s" % (median(data2)))
print("Median of data-set 3 is % s" % (median(data3)))
print("Median of data-set 4 is % s" % (median(data4)))
print("Median of data-set 5 is % s" % (median(data5)))

Producción : 
 

Median of data-set 1 is 5
Median of data-set 2 is 5.9
Median of data-set 3 is 2
Median of data-set 4 is -5
Median of data-set 5 is 0.0

  
Código #3: Demostración de error de estadísticas 
 

# Python code to demonstrate
# StatisticsError of median()
 
# importing the statistics module
from statistics import median
 
# creating an empty data-set
empty = []
 
# will raise StatisticsError
print(median(empty))

Producción : 
 

Traceback (most recent call last):
  File "/home/3c98774036f97845ee9f65f6d3571e49.py", line 12, in 
    print(median(empty))
  File "/usr/lib/python3.5/statistics.py", line 353, in median
    raise StatisticsError("no median for empty data")
statistics.StatisticsError: no median for empty data

  
Aplicaciones: 
Para aplicaciones prácticas, se comparan diferentes medidas de dispersión y tendencia de la población sobre la base de qué tan bien se pueden estimar los valores de población correspondientes. Por ejemplo, una comparación muestra que la media de la muestra es estadísticamente más eficiente que la mediana de la muestra cuando los datos no están contaminados por datos de distribución de datos con colas intensas o de mezclas de distribución de datos, pero menos eficiente de lo contrario y que la eficiencia de la mediana de la muestra es mayor que la de una amplia gama de distribuciones. Para ser más específicos, la mediana tiene una eficiencia del 64 % en comparación con la media de varianza mínima (para muestras normales grandes).