función scipy stats.kurtosis() | Python

La función scipy.stats.kurtosis(array, axis=0, fisher=True, bias=True) calcula la curtosis (Fisher o Pearson) de un conjunto de datos. Es el cuarto momento central dividido por el cuadrado de la varianza. Es una medida de la «continuidad», es decir, un descriptor de la forma de la distribución de probabilidad de una variable aleatoria de valor real. En términos simples, se puede decir que es una medida de cuán pesada es la cola en comparación con una distribución normal. Su fórmula –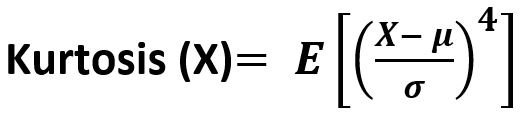

Parámetros: array: Array de entrada u objeto que tiene los elementos. eje : Eje a lo largo del cual se medirá el valor de la curtosis. Por defecto eje = 0. fisher : Bool; Se usa la definición de Fisher (normal 0.0) si es Verdadero; de lo contrario, se utiliza la definición de Pearson (normal 3.0) si se establece en False. sesgo : Bool; los cálculos se corrigen por sesgo estadístico, si se establece en False. Devuelve: valor de curtosis de la distribución normal para el conjunto de datos.

Código #1: 

# Graph using numpy.linspace()
# finding kurtosis
 
from scipy.stats import kurtosis
import numpy as np
import pylab as p
 
x1 = np.linspace( -5, 5, 1000 )
y1 = 1./(np.sqrt(2.*np.pi)) * np.exp( -.5*(x1)**2  )
 
p.plot(x1, y1, '*')
 
 
print( '\nKurtosis for normal distribution :', kurtosis(y1))
 
print( '\nKurtosis for normal distribution :',
      kurtosis(y1, fisher = False))
 
print( '\nKurtosis for normal distribution :',
      kurtosis(y1, fisher = True))

Producción :

Kurtosis for normal distribution : -0.3073930877422071

Kurtosis for normal distribution : 2.692606912257793

Kurtosis for normal distribution : -0.3073930877422071