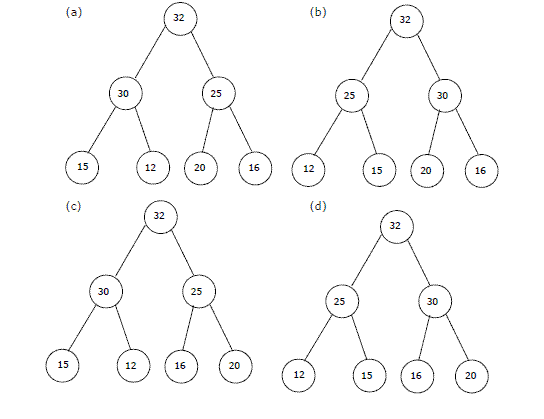
Los elementos 32, 15, 20, 30, 12, 25, 16 se insertan uno por uno en el orden indicado en un Max Heap. El Max Heap resultante es.
(A) a
(B) b
(C) c
(D) d
Answer: (A)
Explanation: A max heap is a complete binary tree in which the value of each non-leaf node is greater than or equal to the values of its children.
Para el caso dado, primero inserte todos los valores en un árbol binario completo. Luego, aplicamos desplazamiento. Lo que hacemos es comenzar con el Node no hoja más inferior. Si es más pequeño que cualquiera (o ambos) de los Nodes secundarios, lo intercambiamos con el secundario más grande. De la misma manera, continuamos moviéndose hacia arriba en el árbol hasta que todos los Nodes que no sean hoja satisfagan las propiedades del montón máximo.
Entonces, la primera vez que hacemos un árbol binario completo, tenemos
32
/ \
15 20
/ \ / \
30 12 25 16
Ahora, necesitamos intercambiar 15 con 30 y 20 con 25.
32
/ \
30 25
/ \ / \
15 12 20 16
Este es el montón máximo requerido y coincide con la opción A.
Entonces, A es la opción correcta.
Comente a continuación si encuentra algo incorrecto en la publicación anterior.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA