PUERTA | PUERTA-CS-2005 | Pregunta 36

En un árbol k-ario completo , cada Node interno tiene exactamente k hijos. El número de hojas en tal árbol con n Nodes internos es
(A) nk
(B) (n – 1)k + 1
(C) n(k – 1) + 1
(D) n(k – 1)

Respuesta: (C)
Explicación:  
Se requieren antecedentes: árboles y relación de recurrencia

Tenemos que abordar este problema formando una relación de recurrencia. Sea T(n) el número de hojas en un árbol que tiene n Nodes internos. Tenemos que relacionar de alguna manera T(n) con T(n-1).

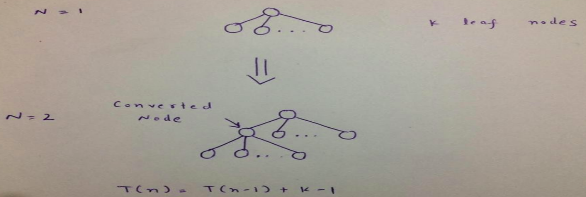
Considere un árbol con n = 1. Este árbol tendrá exactamente k hojas.

Intente crear un árbol con 2 Nodes internos del árbol anterior. Tenemos que hacer que un Node de hoja sea un Node interno y mientras hacemos esto, obtenemos más k hojas. Por lo tanto, el número de Nodes hoja en el árbol recién construido será uno menos que el árbol original, ya que hemos cambiado una hoja a Node interno más k (el Node recién convertido ahora genera k hojas más).

Thus, T(n)   = T(n-1) - 1 + k = T(n-1) + k -1
             = T(n-2) + 2*(k-1)         Solving By Substitution Method
         = T(n-3) + 3*(k-1)
         .
         .
         .
         = T(n-(n-1)) + (n-1)*(k-1)     
         = T(1) + (n-1)*(k-1)
         = k + (n-1)*(k-1)             Forming Base Case : T(1) = k
             = n(k – 1) + 1

En Gate, le sugeriremos que resuelva esta pregunta tomando 2-3 ejemplos y eliminando las opciones. Pero en las entrevistas posteriores, es posible que deba mostrarles cómo forma y resuelve la relación de recurrencia.

Esta explicación ha sido aportada por Pranjul Ahuja.

Visite el siguiente enlace para obtener más información sobre la relación de recurrencia:

Video conferencia del MIT sobre notación asintótica | Recurrencias | Sustitución, método maestro

Cuestionario de esta pregunta