PUERTA | PUERTA CS 2008 | Pregunta 21

El número mínimo de subintervalos de igual longitud necesarios para aproximarse a una precisión de al menos usando la regla trapezoidal es
(A) 1000 l
(B) 1000
(C) 100 l
(D) 100

Respuesta: (A)
Explicación: error de la regla trapezoidal:
$E_n = -\frac{(ba)^3}{12N^2}f^{''}(c)$

Error máximo = 1/3 * 10^{-6} (dado)

Por lo tanto, |Es| < 1/3 * 10^{-6}
a = 1 y b = 2 (dado)

Por lo tanto,

$N^2 > \frac{(b-a)^3}{12*\frac{1}{3}*10^{-6}}|f^n(c)| = \frac{(2-1)^3}{4*10^{-6}}|f^n(c)| = \frac{10^6}{4}|f^n(c)$
$N > \frac{10^3}{2}\sqrt{|f^n(c)|}$

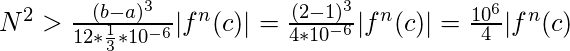
f ^” (x) = xe^x + 2e^x

f ^” (x) es máxima en x=2.
Por lo tanto, f ^” (x) = 4e^2

$N > \frac{10^3}{2}\sqrt{4e^2} = \frac{10^3}{2}*2e = 1000e$

Por lo tanto, la opción (A) es correcta.

Referencia: http://www.cse.iitd.ac.in/~mittal/gate/gate_math_2008.html

Comente a continuación si encuentra algo incorrecto en la publicación anterior.
Cuestionario de esta pregunta

Publicación traducida automáticamente

Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta