Relaciona los siguientes NFA con las expresiones regulares a las que corresponden
1. ϵ + 0(01*1 + 00) * 01* 2. ϵ + 0(10 *1 + 00) * 0 3. ϵ + 0(10 *1 + 10) *1 4. ϵ + 0(10 *1 + 10) *10 *

(A) P – 2, Q – 1, R – 3, S – 4
(B) P – 1, Q – 3, R – 2, S – 4
(C) P – 1, Q – 2, R – 3 , S – 4
(D) P – 3, Q – 2, R – 1, S – 4
Respuesta: (C)
Explicación: Truco: Aquí vemos en todas las figuras dadas que el segundo estado tiene un bucle sobre los alfabetos de entrada. En tales casos, deberíamos resolver el ciclo en ese estado y transformar el NFA en uno más simple para obtener una expresión regular para el NFA.
Para resolver el bucle, primero llegue al estado donde se va a resolver el bucle y luego dibuje todos los bucles sobre ese estado y todos los movimientos posibles para pasar al estado final.
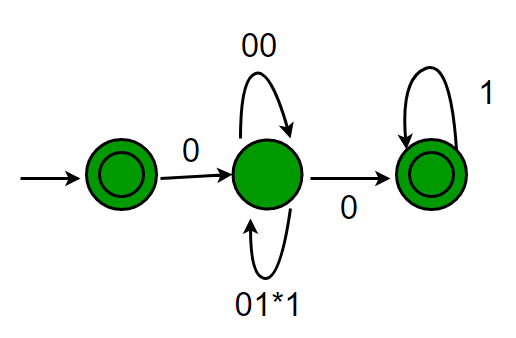
Figure P: (when loop resolved at middle state)
El bucle en el estado medio es un 00 o un 01*1.
De ahí la expresión regular: € + 0(00 +01*1)* 01*
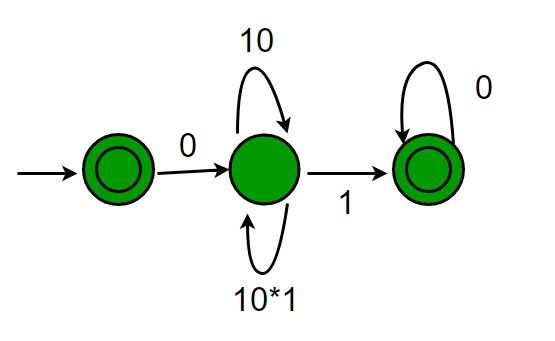
Figure Q: (when loop resolved at middle state)
El bucle en el estado medio es un 00 o un 10*1.
De ahí la expresión regular: € + 0(00 +10*1)* 0.
Figure R: (when loop resolved at middle state)
El bucle en el estado medio es un 10 o un 10*1.

De ahí la expresión regular: € + 0(10 +10*1)* 1.
Figure S: (when loop resolved at middle state)
El bucle en el estado medio es un 10 o un 10*1.
De ahí la expresión regular: € + 0(10 +10*1)* 10*.
Las expresiones regulares que coinciden con las anteriores dan una coincidencia adecuada como P-1, Q-2, R-3, S-4
Esta explicación ha sido aportada por Yashika Arora.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA