PUERTA | PUERTA-CS-2009 | Pregunta 35

El tiempo de ejecución de un algoritmo está representado por la siguiente relación de recurrencia:

    if  n <= 3  then   T(n) = n
    else T(n) = T(n/3) + cn

¿Cuál de los siguientes representa la complejidad temporal del algoritmo? <pre>
(A) (n)
(B) (n log n)
(C) (n^2)
(D) (n^2log n) </pre>

 
(A) A
(B) B
(C) C
(D) D

Respuesta: (A)
Explicación:

Respuesta (A)

T(n) = cn + T(n/3)
     = cn + cn/3 + T(n/9)
     = cn + cn/3 + cn/9 + T(n/27)
Taking the sum of infinite GP series. The value of T(n) will
be less than this sum.
T(n) <= cn(1/(1-1/3))
     <= 3cn/2

or we can say 
cn <= T(n) <= 3cn/2
Therefore T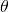(n) = (n)

Esto también se puede resolver usando  el Teorema Maestro  para resolver recurrencias. La expresión dada se encuentra en  el Caso 3  del teorema.

Cuestionario de esta pregunta