PUERTA | PUERTA CS 2012 | Pregunta 65 – Part 5

¿Cuáles de las siguientes afirmaciones son CORRECTAS?
P: Agregar 7 a cada entrada en una lista agrega 7 a la media de la lista
P: Agregar 7 a cada entrada en una lista agrega 7 a la desviación estándar de la lista
R: Duplicar cada entrada en una lista duplica la media de la lista
S: Duplicar cada entrada en una lista deja la desviación estándar de la lista sin cambios
(A) P, Q
(B) Q, R
(C) P, R
(D) R, S

Respuesta: (C)
Explicación: La media es promedio.

Let us consider below example


These eight data points have the mean (average) of 5:


When we add 7 to all numbers, mean becomes 12 so P is TRUE.

If we double all numbers mean becomes double, so R is also
TRUE.

Standard Deviation is square root of variance.
Variance is sum of squares of differences between all numbers
and means.

Deviation for above example
First, calculate the deviations of each data point from the mean, 
and square the result of each:







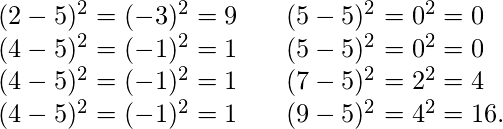
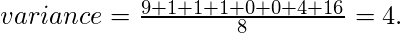
If we add 7 to all numbers, standard deviation won't change 
as 7 is added to mean also. So Q is FALSE.

If we double all entries, standard deviation also becomes 
double.  So S is false.