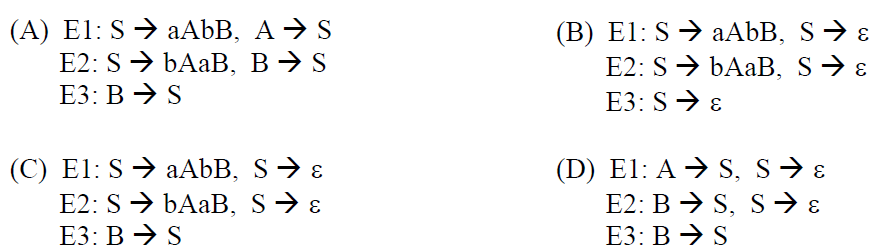PUERTA | PUERTA CS 2012 | Pregunta 65 – Part 9

Considere la fecha igual que la pregunta anterior . Las entradas apropiadas para E1, E2 y E3 son

(A) A
(B) B
(C) C
(D) D

Respuesta: (C)
Explicación:
Como necesitamos encontrar las entradas E1, E2 y E3 que están contra los no terminales S y B, trataremos solo con aquellos producciones que tienen S y B en LHS.

Aquí representamos la tabla de análisis como M[ X , Y ], donde X representa filas (no terminales) e Y representa columnas (terminales).

Rule 1: if P --> Q is a production, for each terminal
        't' in FIRST(Q) add P-->Q to M [ P , t ]

Rule 2 : if epsilon is in FIRST(Q), add P --> Q to
         M [ P , f ] for each f in FOLLOW(P). 

Para la regla de producción S–> aAbB, se agregará a la tabla de análisis en la posición M[ S , PRIMERO( aAbB ) ], ahora PRIMERO(aAbB) = {a}, por lo tanto agregue S–> aAbB a M[ S , a] que es E1.

Para la regla de producción S–> bAaB, se agregará a la tabla de análisis en la posición M[ S , PRIMERO( bAaB ) ], ahora PRIMERO(bAaB) = {b}, por lo tanto agregue S–> bAaB a M[ S , b] que es E2

Para la regla de producción S–> epsilon , se agregará a la tabla de análisis en la posición M[ S , FOLLOW(S) ], ahora FOLLOW(S) = { a , b , $}, por lo tanto agregue S –> epsilon a M[ S , a ] y M[ S , b ] que son nuevamente E1 y E2 respectivamente.

Para la regla de producción B –> S, se agregará a la tabla de análisis en la posición M[ B , FIRST(S ) ], ahora FIRST(S) también contiene épsilon, por lo tanto agregue B –> S a M[ S , FOLLOW (B) ], y FOLLOW(B) contiene {$}, es decir, M[ S , $] que es E3.

epsilon corresponde a una string vacía.

Cuestionario de esta pregunta