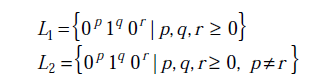PUERTA | PUERTA CS 2013 | Pregunta 32

Considere los siguientes idiomas.

¿Cuál de las siguientes afirmaciones es falsa?
(A) L2 es independiente del contexto.
(B) L1 intersección L2 es independiente del contexto.
(C) El complemento de L2 es recursivo.
(D) El complemento de L1 no tiene contexto pero no es regular.

Respuesta: (D)
Explicación: (D) es falso.

L1 es regular, por lo que su complemento también sería regular.

L1 es un lenguaje regular de la forma 0^* 1^* 0^*. L2, por otro lado, es una CFL, ya que puede derivarse de la siguiente CFG
L2 = { 0^p 1^q 0^r | p,q,r>0 And p notEqualTo r }
S -> AC|CA
C -> 0C0|B
A -> 0A|0
B -> 1B|epsilon
Si es difícil encontrar un CFG para L2, uno puede intuitivamente ver eso reduciéndolo a un problema más simple. L2 es muy similar a una LFC conocida L3 = { a^mb^l | m no es igual a n }

(A) L2 no tiene contexto, lo cual es cierto [CORRECTO]
(B) La intersección de L1 L2 no tiene contexto, lo que también es cierto porque L1 es un lenguaje regular y L2 es un CFL. RL union CFL es siempre una CFL. Por lo tanto, [CORRECTO]
(C) El complemento de L2 es recursivo, lo cual es cierto debido al hecho de que el complemento de un CFL es seguro CSL (lenguaje sensible al contexto), que a su vez (CSL) es un subconjunto de lenguajes recursivos. Por lo tanto [CORRECTO]
(D) El complemento de L1 está libre de contexto pero no es regular, lo cual es falso debido a las leyes de clausura de los lenguajes regulares. El complemento de una RL es siempre una RL. Por lo tanto [INCORRECTO]

Esta solución es aportada por .
Cuestionario de esta pregunta