PUERTA | GATE-CS-2015 (Conjunto 1) | Pregunta 44

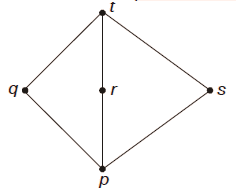
Supongamos que L = {p, q, r, s, t} es una red representada por el siguiente diagrama de Hasse:

Para cualquier x, y ∈ L, no necesariamente distintas, x ∨ y yx ∧ y son unión y reunión de x, y respectivamente. Sea L ³ = {(x,y,z): x, y, z ∈ L} el conjunto de todos los tripletes ordenados de los elementos de L. Sea pr la probabilidad de que un elemento (x,y,z) ∈ L ³ elegido satisface equiprobablemente x ∨ (y ∧ z) = (x ∨ y) ∧ (x ∨ z). Entonces
(A) Pr = 0
(B) Pr = 1
(C) 0 < Pr ≤ 1/5
(D) 1/5 < Pr < 1

Respuesta: (D)
Explicación:

Number of triplets in L3 = Number of ways in which 
                             we can choose 3 elements 
                             from 5 with repetition 

                              = 5 * 5 * 5 
                              = 125.

Now, when we take x = t, then the given condition for L is
satisfied for any y and z. Here, y and z can be taken in 
5 * 5 = 25 ways.

Take x = r, y = p, z = p. Here also, the given condition is
satisfied. So, pr > 25 / 125 > 1/5.

For x = q, y = r, z = s, the given condition is not satisfied
as q ⋁ (r ⋀ s) = q ⋁ p = q, while (q ⋁ r) ⋀ (q ⋁ s) = t ⋀ t = t.

So, pr ≠ 1.

Hence  D choice.

Cuestionario de esta pregunta