Respuesta: (A)
Explicación: Dado- ![]()
Poniendo ![]() obtenemos-
obtenemos- ![]()
Restando la segunda ecuación de la primera obtenemos- Volviendo 
a poner este valor en la primera ecuación- 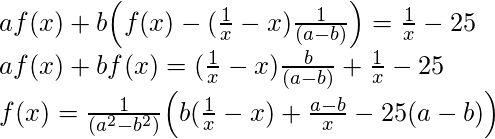
Ahora que tenemos ![]() podemos encontrar
podemos encontrar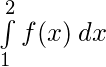
![Rendered by QuickLaTeX.com \begin{flalign*} \int f(x)\:dx &= \int \frac{1}{(a^2-b^2)} \Big( b(\frac{1}{x}-x) + \frac{a-b}{x} - 25(a-b)\Big)\:dx \\ &= \frac{1}{(a^2-b^2)} \Big( b(\ln{x}-\frac{x^2}{2}) + (a-b)\ln{x} - 25(a-b)x\Big) \\ &= \frac{1}{(a^2-b^2)} \Big( \frac{-bx^2}{2} + a\ln{x} - 25(a-b)x\Big) \\ &\text{Putting the limits}\\ &= \frac{1}{(a^2-b^2)} \Big[ \frac{-bx^2}{2} + a\ln{x} - 25(a-b)x\Big] \limits_{1}^{2} \\ &= \frac{1}{(a^2-b^2)} \Big[ \big(-2b + a\ln{2} - 50(a-b)\big) - \big(-\frac{b}{2} + 0 - 25(a-b)\big) \Big] \\ &= \frac{1}{(a^2-b^2)} \Big( \frac{-3b}{2} + a\ln{2} - 25(a-b)\Big) \\ &= \frac{1}{(a^2-b^2)} \Big( \frac{47b}{2} + a(\ln{2} - 25)\Big) \\ \end{flalign*}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ee416288ffe41af277877bf43b16dd32_l3.png)
Por lo tanto, la opción correcta es A.
Cuestionario de esta pregunta
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA
