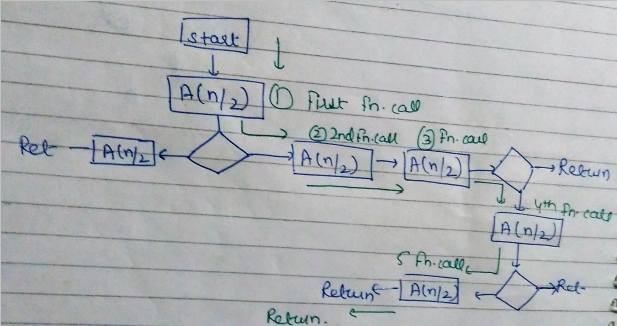
El diagrama dado muestra el diagrama de flujo para una función recursiva A(n). Suponga que todas las sentencias, excepto las llamadas recursivas, tienen una complejidad de tiempo O(1). Si la complejidad temporal del caso más desfavorable de esta función es O(n α ), entonces el valor mínimo posible (con una precisión de hasta dos posiciones decimales) de α es __________ (A) 2,2 a 2,4 (B) 3,2 a 3,4 (C) 0 a 1.8 (D) 1 Respuesta: (A) Explicación: La complejidad temporal de una relación de recurrencia es la complejidad temporal del peor de los casos. Primero tenemos que averiguar el número de llamadas de función en el peor de los casos a partir del diagrama de flujo.
El peor de los casos será cuando todas las condiciones (cajas de diamantes) resulten en caminos sin retorno que tengan la raíz más larga. En el camino más largo tenemos 5 llamadas a funciones.
Entonces, la relación de recurrencia será:
A(n) = 5A(n/2) + O(1) (O(1) porque el resto de las declaraciones tienen una complejidad de O(1).)
Resolviendo esta relación de recurrencia usando el teorema de Master:
a = 5 , b= 2 , f(n) =O(1) , n log b a = n log 2 5 (caso 1 teorema maestro)
A(n) =n log b a
valor de log 2 5 es 2.3219, entonces , la mejor opción es la opción a
Esta explicación ha sido aportada por Parul Sharma.
Cuestionario de esta pregunta
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA