PUERTA | GATE-CS-2017 (Conjunto 1) | Pregunta 17

Sea T un árbol de búsqueda binario con 15 Nodes. Las alturas mínimas y máximas posibles de T son:

Nota: La altura de un árbol con un solo Node es 0.
(A) 4 y 15 respectivamente
(B) 3 y 14 respectivamente
(C) 4 y 14 respectivamente
(D) 3 y 15 respectivamente

Respuesta: (B)
Explicación:

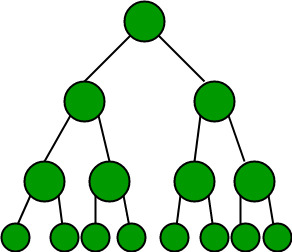
• La altura mínima de un árbol de búsqueda binaria será cuando el árbol esté completo:

  

  Ahora, sea h la altura del árbol binario, entonces, 2^{0}+2^{1}+2^{2}+2^{3}+…+2^{h}=2^{h +1}-1 <= n
  Entonces, altura mínima de un árbol de búsqueda binaria = log ₂ (n+1) – 1 = log ₂ (15+1) – 1 = 4 – 1 = 3

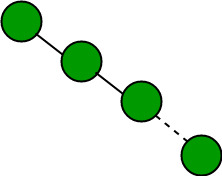
• La altura máxima de un árbol de búsqueda binaria será cuando el árbol esté completamente sesgado: (como a continuación)

  

  Altura máxima del árbol de búsqueda binaria = n-1 = 15 – 1 = 14, donde el árbol es un árbol sesgado

Por lo tanto, la opción B 

Cuestionario de esta pregunta