Sea G = (V, E) cualquier gráfico ponderado de borde no dirigido conectado. Los pesos de las aristas en E son positivos cualquier distinto. Considere las siguientes declaraciones:
I. Minimum Spanning Tree of G is always unique. II. Shortest path between any two vertices of G is always unique.
¿Cuál de las afirmaciones anteriores es/son necesariamente verdaderas?
(A) solo I
(B) solo II
(C) tanto I como II
(D) ni I ni II
Respuesta: (A)
Explicación: I. El árbol de expansión mínimo de G siempre es único: MST siempre será distinto si los bordes son únicos así que Correcto
II. El camino más corto entre dos vértices de G siempre es único: el camino más corto entre dos vértices puede ser el mismo, por lo que es incorrecto
Por lo tanto , la opción A es correcta.
Solución alternativa:
sabemos que el árbol de expansión mínimo de un gráfico siempre es único si todos los pesos son distintos, por lo que la afirmación 1 es correcta.
Ahora declaración 2, esto podría no ser cierto en todos los casos. Considere el gráfico. Hay dos caminos más cortos de a a b (uno es directo y otro a través del Node c) Por lo tanto, la declaración 2 es falsa. Por lo tanto, la opción a es correcta. Cuestionario de esta pregunta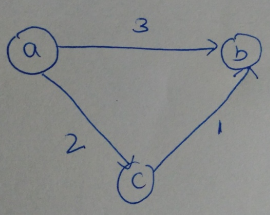
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA