El gráfico G se obtiene sumando el vértice s a K 3,4 y haciendo que s sea adyacente a cada vértice de K 3,4 . El número mínimo de colores necesarios para el color de borde G es _________ .
Nota: esta pregunta era de tipo numérico.
(A) 2
(B) 3
(C) 5
(D) 7
Respuesta: (D)
Explicación: tenga en cuenta la pregunta sobre el color de los bordes pero no sobre el color de los vértices.
Entonces, de acuerdo con la coloración de los bordes de un gráfico, es una asignación de «colores» a los bordes del gráfico para que no haya dos bordes adyacentes que tengan el mismo color con una cantidad óptima de colores.
Se requiere un mínimo de 4 colores para colorear los bordes del gráfico K 3,4 , porque un máximo de 4 bordes inciden en algunos vértices.
Para el grafo modificado, 4 aristas de diferente color serán incidentes en el vértice “s”, ahora de otro conjunto de 3 vértices de K 3,4 también serán incidentes el mismo vértice “s”. Entonces, para preservar la propiedad del color del borde, necesitamos 3 colores más para colorear este gráfico modificado.
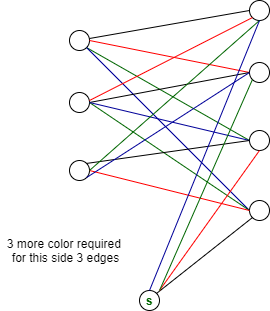
Por lo tanto, la respuesta será 4+3 = 7 colores.
La opción (D) es correcta.
Publicación traducida automáticamente
Artículo escrito por GeeksforGeeks-1 y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA