Genere un gráfico usando Diccionario en Python

Requisito previo – Gráficos 
Para dibujar gráficos usando bibliotecas integradas – Trazado de gráficos en Python
En este artículo, veremos cómo implementar gráficos en python usando la estructura de datos del  diccionario en python.
Las claves del diccionario utilizado son los Nodes de nuestro gráfico y los valores correspondientes son listas con cada Node, que se conectan por un borde. 

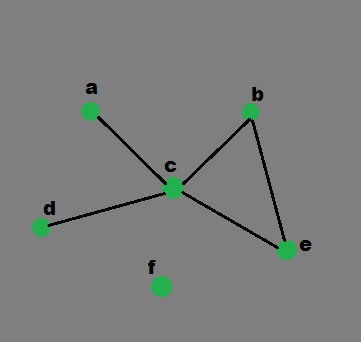
Este gráfico simple tiene seis Nodes (af) y cinco arcos: 

a -> c
b -> c
b -> e
c -> a
c -> b
c -> d
c -> e
d -> c
e -> c
e -> b

Se puede representar mediante la siguiente estructura de datos de Python. Este es un diccionario cuyas claves son los Nodes del grafo. Para cada clave, el valor correspondiente es una lista que contiene los Nodes que están conectados por un arco directo desde este Node. 

graph = { "a" : ["c"],
          "b" : ["c", "e"],
          "c" : ["a", "b", "d", "e"],
          "d" : ["c"],
          "e" : ["c", "b"],
          "f" : []
        } 

Representación gráfica del ejemplo anterior: 
 

defaultdict : por lo general, un diccionario de Python arroja un KeyError si intenta obtener un elemento con una clave que no está actualmente en el diccionario. defaultdict permite que si una clave no se encuentra en el diccionario, en lugar de arrojar un KeyError, se crea una nueva entrada. El tipo de esta nueva entrada viene dado por el argumento de defaultdict. 

Función Python para generar gráfico: 

# definition of function
def generate_edges(graph):
    edges = []

    # for each node in graph
    for node in graph:

        # for each neighbour node of a single node
        for neighbour in graph[node]:
            # if edge exists then append
            edges.append((node, neighbour))
    return edges

Implementación:

# Python program for 
# validation of a graph
  
# import dictionary for graph
from collections import defaultdict
  
# function for adding edge to graph
graph = defaultdict(list)
def addEdge(graph,u,v):
    graph[u].append(v)
  
# definition of function
def generate_edges(graph):
    edges = []
  
    # for each node in graph
    for node in graph:
          
        # for each neighbour node of a single node
        for neighbour in graph[node]:
              
            # if edge exists then append
            edges.append((node, neighbour))
    return edges
  
# declaration of graph as dictionary
addEdge(graph,'a','c')
addEdge(graph,'b','c')
addEdge(graph,'b','e')
addEdge(graph,'c','d')
addEdge(graph,'c','e')
addEdge(graph,'c','a')
addEdge(graph,'c','b')
addEdge(graph,'e','b')
addEdge(graph,'d','c')
addEdge(graph,'e','c')
  
# Driver Function call 
# to print generated graph
print(generate_edges(graph)) 

[('a', 'c'), ('b', 'c'), ('b', 'e'), ('c', 'd'), 
  ('c', 'e'), ('c', 'a'), ('c', 'b'), ('e', 'b'), 
  ('e', 'c'), ('d', 'c')]

Como hemos tomado un ejemplo de gráfico no dirigido, hemos impreso el mismo borde dos veces, como (‘a’, ‘c’) y (‘c’, ‘a’). Podemos superar esto con el uso de gráficos dirigidos. 
A continuación hay algunos programas más en gráficos en python: 
 
Para generar la ruta de un Node al otro Node : 

Usando el diccionario de Python, podemos encontrar la ruta de un Node al otro en un gráfico. La idea es similar a DFS en gráficos. 
En la función, inicialmente, la ruta es una lista vacía. Al principio, si el Node inicial coincide con el Node final, la función devolverá la ruta. De lo contrario, el código avanza y alcanza todos los valores del Node inicial y busca la ruta mediante la recursividad. 

# Python program to generate the first
# path of the graph from the nodes provided
  
graph = {
    'a': ['c'],
    'b': ['d'],
    'c': ['e'],
    'd': ['a', 'd'],
    'e': ['b', 'c']
}
  
# function to find path
  
  
def find_path(graph, start, end, path=[]):
    path = path + [start]
    if start == end:
        return path
    for node in graph[start]:
        if node not in path:
            newpath = find_path(graph, node, end, path)
            if newpath:
                return newpath
  
  
# Driver function call to print the path
print(find_path(graph, 'd', 'c'))

['d', 'a', 'c']

Programa para generar todos los caminos posibles de un Node al otro. : 

En el programa discutido anteriormente, generamos la primera ruta posible. Ahora, generemos todos los caminos posibles desde el Node inicial hasta el Node final. El funcionamiento básico funciona igual que el funcionamiento del código anterior. El lugar donde surge la diferencia es que, en lugar de devolver instantáneamente la primera ruta, guarda esa ruta en una lista denominada ‘rutas’ en el ejemplo que se muestra a continuación. Finalmente, después de iterar sobre todas las formas posibles, devuelve la lista de rutas. Si no hay una ruta desde el Node inicial hasta el Node final, devuelve Ninguno. 

Implementación:

# Python program to generate the all possible
# path of the graph from the nodes provided
graph ={
'a':['c'],
'b':['d'],
'c':['e'],
'd':['a', 'd'],
'e':['b', 'c']
}
  
# function to generate all possible paths
def find_all_paths(graph, start, end, path =[]):
  path = path + [start]
  if start == end:
    return [path]
  paths = []
  for node in graph[start]:
    if node not in path:
      newpaths = find_all_paths(graph, node, end, path)
    for newpath in newpaths:
      paths.append(newpath)
  return paths
    
# Driver function call to print all 
# generated paths
print(find_all_paths(graph, 'd', 'c'))

[['d', 'a', 'c'], ['d', 'a', 'c']]

Programa para generar el camino más corto. : 

Para llegar al más corto de todos los caminos, usamos un enfoque un poco diferente, como se muestra a continuación. En esto, a medida que obtenemos la ruta desde el Node inicial hasta el Node final, comparamos la longitud de la ruta con una variable denominada como la más corta que se inicializa con el valor Ninguno. Si la longitud de la ruta generada es menor que la longitud de la más corta, si la ruta más corta no es Ninguno, la ruta recién generada se establece como el valor de la más corta. Nuevamente, si no hay ruta, devuelve Ninguno 

Implementación:

# Python program to generate shortest path
  
graph ={
'a':['c'],
'b':['d'],
'c':['e'],
'd':['a', 'd'],
'e':['b', 'c']
}
  
# function to find the shortest path
def find_shortest_path(graph, start, end, path =[]):
        path = path + [start]
        if start == end:
            return path
        shortest = None
        for node in graph[start]:
            if node not in path:
                newpath = find_shortest_path(graph, node, end, path)
                if newpath:
                    if not shortest or len(newpath) < len(shortest):
                        shortest = newpath
        return shortest
          
# Driver function call to print
# the shortest path
print(find_shortest_path(graph, 'd', 'c'))

['d', 'a', 'c']

Este artículo es una contribución de Shivam Pradhan (anuj_charm) y Rishabh Bansal . Si te gusta GeeksforGeeks y te gustaría contribuir, también puedes escribir un artículo usando write.geeksforgeeks.org o enviar tu artículo por correo a review-team@geeksforgeeks.org. Vea su artículo que aparece en la página principal de GeeksforGeeks y ayude a otros Geeks.