Geometría GRE | Líneas y ángulos

Líneas:
Una línea es una figura geométrica unidimensional que tiene un ancho insignificante que se extiende infinitamente en ambas direcciones. Una línea puede ser recta o curva.
Una línea recta tiene la misma dirección en toda su longitud de un punto a otro.
Una línea curva cambia su dirección continuamente de un punto a otro.

Segmento de línea:
un segmento de línea es una parte de una línea que tiene puntos finales específicos. Puede haber un número infinito de segmentos de línea en una línea. En el siguiente diagrama, AB es un segmento de línea denotado. Dos segmentos de línea que tienen la misma longitud se llaman segmentos de línea congruentes .

Tipos de Líneas:

1. Las líneas horizontales son paralelas al eje x del plano bidimensional
   
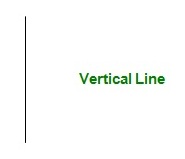
2. Las líneas verticales son paralelas al eje y del plano bidimensional
   
3. Líneas paralelas: si la distancia entre dos líneas rectas permanece igual a lo largo de su longitud en todos los puntos, se dice que son paralelas. En otras palabras, no se cruzan en ningún lugar del plano.
   
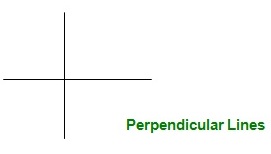
4. Líneas perpendiculares: si una línea horizontal y una vertical se cruzan en un plano, son perpendiculares.
   

Ángulos:
Cuando dos rectas se cortan en un punto, se dice que forman un ángulo . Se puede medir en grados o radianes. Las rectas se llaman brazos del ángulo y el punto de intersección se llama vértice .

Tipos de ángulos:

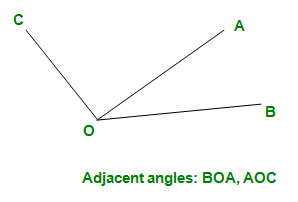
1. Ángulos adyacentes: ángulos que se encuentran a ambos lados de un brazo común. En la siguiente figura, los ángulos BOA y AOC son adyacentes y tienen un brazo común OA
   
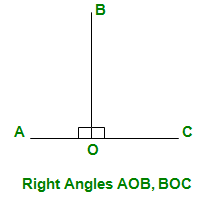
2. Ángulo recto: cuando los ángulos adyacentes son iguales entre sí para dos líneas que se cruzan, cada uno de los ángulos se llama ángulo recto, indicado por 90 ^o (representado como un pequeño cuadrado)
   
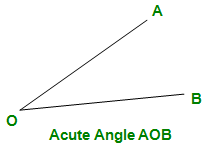
3. Ángulo agudo: un ángulo que es menor que un ángulo recto (menos de 90 ^o ) se llama ángulo agudo
   
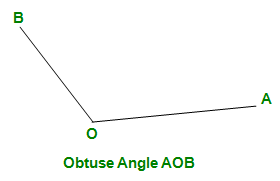
4. Ángulo obtuso: un ángulo que es mayor que un ángulo recto (mayor que 90 ^o ) se llama ángulo obtuso
   
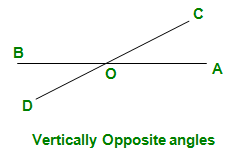
5. Ángulos verticalmente opuestos: cuando dos líneas rectas se intersecan y se cruzan en O, los ángulos AOC y DOB son verticalmente opuestos. Los ángulos DOA y BOC también son verticalmente opuestos entre sí. Además, estos ángulos tienen la misma medida ( ángulos congruentes )
   
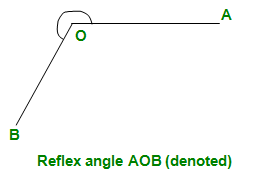
6. Ángulo reflejo: se dice que un ángulo que es mayor que dos ángulos rectos pero menor que cuatro ángulos rectos es reflejo
   
7. Ángulos suplementarios: se dice que dos ángulos cuya suma es dos ángulos rectos son suplementarios.
   
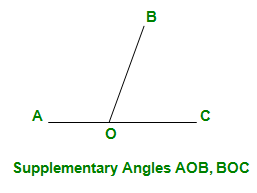
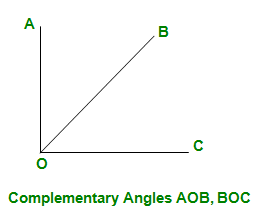
8. Ángulos complementarios: se dice que dos ángulos cuya suma es un ángulo recto son complementarios.
   

Bisectriz de ángulo:
si dos ángulos adyacentes son iguales, entonces el brazo del segmento de línea común a ambos ángulos se conoce como bisectriz de ángulo.

Ejemplos:

Ejemplo-1: En la figura que se muestra a continuación, se da que el ángulo BOC es un ángulo recto y el ángulo JHC es 30 ^o . Además, las líneas AJ y DI son paralelas. Encuentra el valor del ángulo OFG.

Solución:
en primer lugar, los ángulos JHC y el ángulo GHE son verticalmente opuestos. Por eso,

angle JHC = angle GHE
=> angle GHE = 30o 

Ahora, las rectas AJ y DI son paralelas; y los ángulos GHE y FGH son suplementarios.

=> angle GHE + angle FGH = 180o
=> angle FGH = 180o - angle GHE
=> angle FGH = 180o - 30o
=> angle FGH = 150o 

Nuevamente, los ángulos FGH y el ángulo OGF son complementarios entre sí.

=> angle FGH + angle OGF = 180o
=> angle OGF = 180o - angle FGH
=> angle OGF = 180o - 150o
=> angle OGF = 30o 

Finalmente, se da el ángulo FOG = 90 ^o , por lo que los ángulos OGF y OFG son complementarios.

So angle OGF + angle OFG = 90o
=> angle OFG = 90o - angle OGF
=> angle OFG = 90o - 30o
=> angle OFG = 60o

Therefore, the desired angle OFG 
= 60o 

Ejemplo-2: En la figura que se muestra a continuación, si x = y + 30 ^o , y AB es paralela a CD. Encuentra el valor del ángulo y.

Solución –
Aplicando el concepto de ángulos verticales, se entiende que,

angle Dxy = angle x 

Ahora los ángulos x e y son suplementarios,

Hence, angle x + angle y = 180o
=> (angle y + 30o) + angle y = 180o
=> 2 * angle y = 180o - 30o
=> angle y = 150o/2
=> angle y = 75o

Therefore, the desired angle y is 75o