Geometría GRE | polígonos

Polígonos:
La palabra polígono se deriva de la palabra griega polugonon, aquí poli significa muchos y gons significa ángulos. Los polígonos se pueden definir como una curva cerrada formada por segmentos de línea. Cada segmento de línea se convertirá en lados del polígono.

Clasificación de los polígonos:
En base al número de lados los polígonos se clasifican de la siguiente manera:

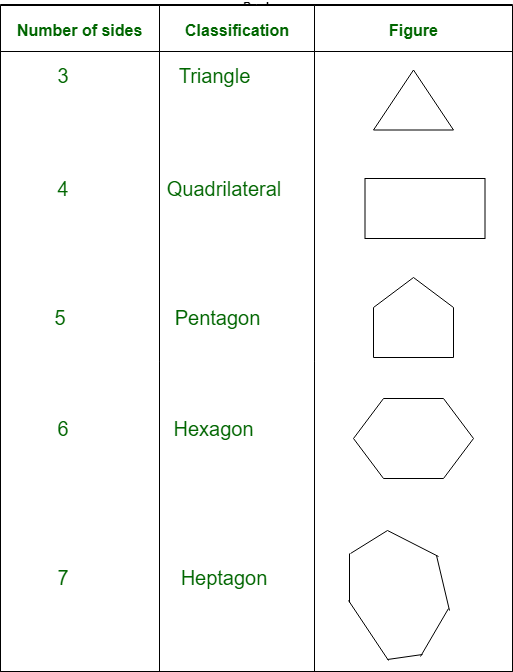
Para n lados, podemos llamarlo n-gon. De aquí podemos observar que el triángulo es un polígono con menor número de lados.

Polígono cóncavo y convexo:
Los polígonos convexos son los polígonos cuyas diagonales se encuentran dentro de la figura y los polígonos cóncavos son aquellos cuyas diagonales se encuentran fuera de la figura.

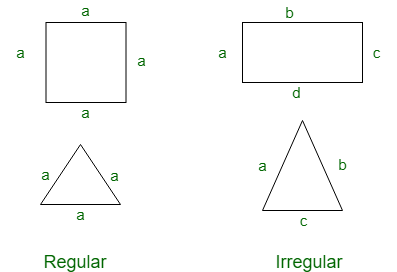
Polígono regular e irregular:
Los polígonos regulares son los polígonos que tienen todos los lados de igual longitud y los polígonos irregulares son los polígonos que tienen lados de diferente longitud.

Nota:

• Para un polígono, ángulo exterior + ángulo interior = 360°
• La suma de todos los ángulos exteriores del polígono es 360°
• En un polígono regular todos los ángulos interiores son iguales.
• En un polígono regular todos los ángulos exteriores también son iguales.
• Para un polígono regular, Número de lados = 360/ángulo exterior.
• La suma de todos los ángulos interiores de un polígono viene dada por (n-2)*180, donde ‘n’ es el número de lados del polígono.
• El área de un polígono significa el área encerrada por el polígono y el perímetro de un polígono es la suma de todas las longitudes de los lados.

Ejemplos:

• Ejemplo-1: ¿Cuál es la suma de todos los ángulos interiores del heptágono?
  Solución:

  Since it is a Heptagon, number of sides (n) = 7
  Sum of all interior angles = (n-1)*180 

  Entonces, para la suma heptágono de los ángulos interiores = (7-2)*180 = 900

• Ejemplo-2: ¿Calcular el número de lados en un polígono regular que tiene un ángulo exterior de 45°?
  Solución:

  Number of sides = 360/exterior angle
  Since exterior angle is 45°
  number of sides = 360/45 = 8 

• Ejemplo-3: ¿Cuál será el valor de un ángulo interior para un hexágono regular?
  Solución:

  Since it is a hexagon, number of sides (n) = 6
  exterior angle = 360°/6 = 60
  we know that, interior angle + exterior angle = 180°
  interior angle + 60° = 180°
  interior angle = 180° - 60° 
  interior angle = 120 ° 

• Ejemplo-4: El ángulo exterior de un polígono regular es 8°.

  (a) find the number of sides in the polygon?
  (b) find the interior angle of the polygon? 

  Solución:

  (a) Number of sides = 360°/8°= 45
  (b) interior angle = 180°- 8° = 172