polígonos
Los polígonos son figuras planas formadas por una serie cerrada de segmentos rectilíneos. Ej : Triángulo, Rectángulo, etc.
Propiedades:
1. Suma de todos los ángulos de un polígono de n lados = (n-2)π
2. Suma de todos los ángulos exteriores = 360°
3. Nº de lados = 360°/ángulo exterior
Clasificación de polígonos –
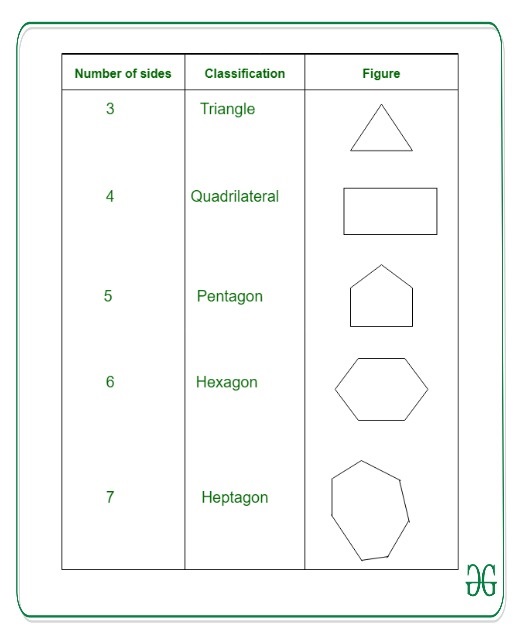
triangulos
Un triángulo es un polígono que tiene tres lados.
Área:
1. Área = 1/2 x base x altura
2. Área = √s(sa)(sb)(sc) donde s = a+b+c/2
3. Área = rs (donde r está dentro del radio )
4. Área = 1/2 x producto de dos lados x seno del ángulo
5. Área = abc/4R donde R = circunradio
Congruencia de Triángulos:
1. Congruencia SAS: Si dos lados y un ángulo incluido de un triángulo son iguales a dos lados y un ángulo incluido de otro, los dos triángulos son congruentes.
2. Congruencia ASA: Si dos ángulos y el lado incluido de un triángulo es igual a dos ángulos y el lado incluido de otro, los triángulos son congruentes.
3. Congruencia AAS: Si dos ángulos y el lado opuesto a uno de los ángulos es igual a los ángulos y lados correspondientes de otro triángulo, los triángulos son congruentes.
4. Congruencia SSS: si los tres lados de un triángulo son iguales a los tres lados de otro triángulo, los dos triángulos son congruentes.
5. Congruencia SSA:Si dos lados y el ángulo opuesto al lado mayor de un triángulo son iguales a los dos lados y el ángulo opuesto al lado mayor de otro triángulo, entonces los triángulos son congruentes.
Semejanza de Triángulos:
1. Semejanza AAA: Si en dos triángulos, los ángulos correspondientes son iguales, entonces los triángulos son semejantes.
2. Semejanza SSS: si los lados correspondientes de dos triángulos son proporcionales, entonces son similares.
3. Semejanza SAS: si en dos triángulos, un par de lados correspondientes son proporcionales y los ángulos incluidos son iguales, entonces los dos triángulos son similares.
Triángulos equiláteros:
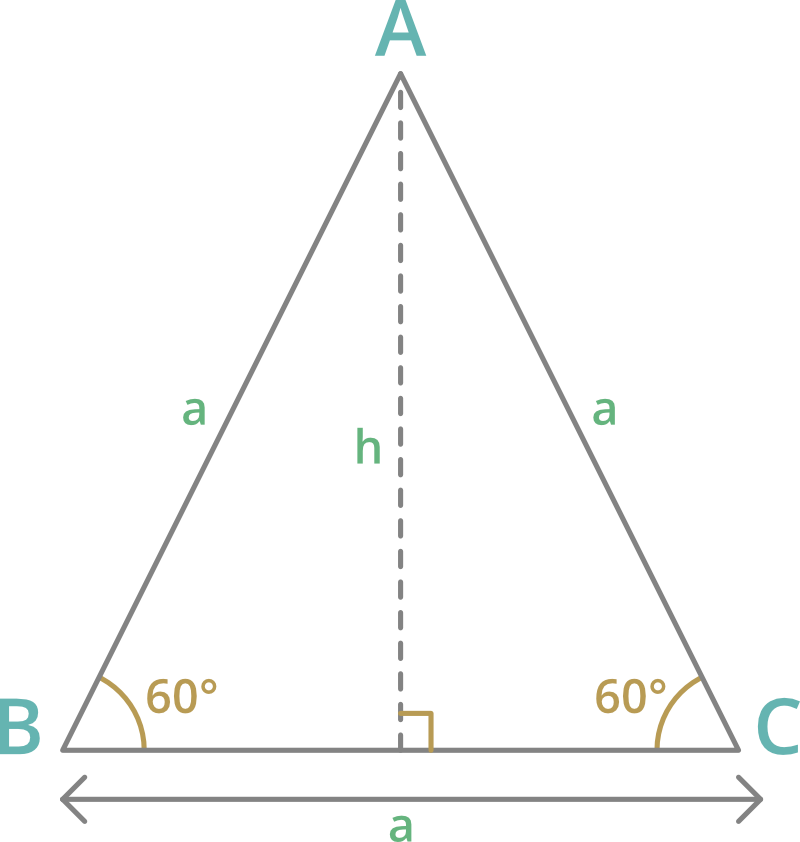
1. Altura = a√3/2
2. Área = √3a 2 /4
3. R(radio de circunvalación) = 2h/3 = a/√3
4. r(en radio) = h/3 = a/2√ 3
5. En el triángulo equilátero coinciden el ortocentro, el centro, el circuncentro y el baricentro.
Triángulo isósceles:
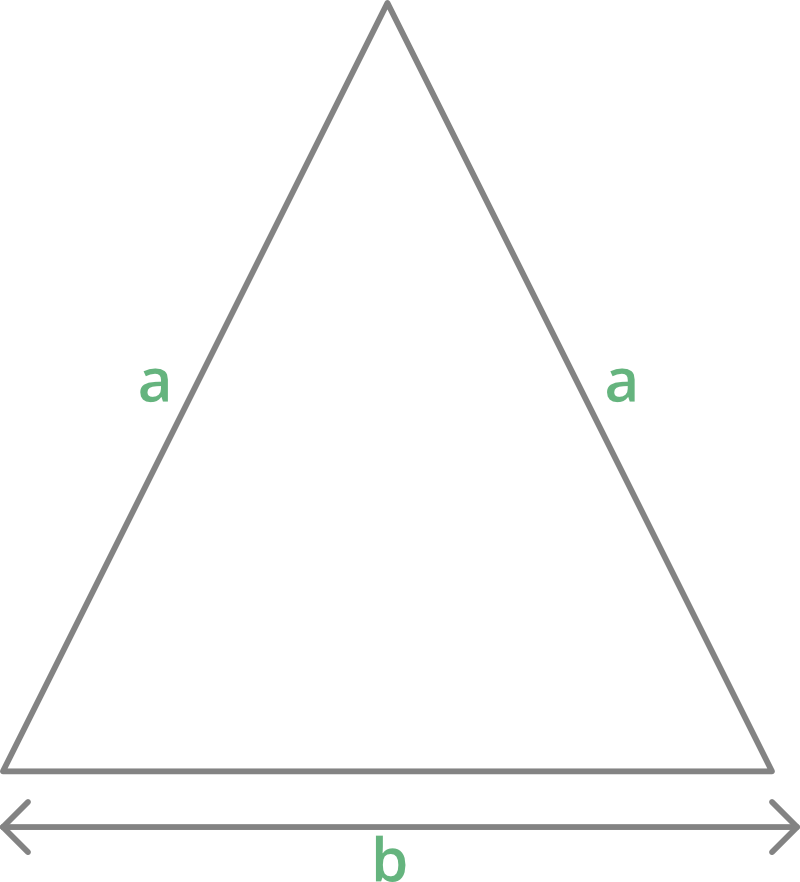
Área = b/4√(4a 2 – b 2 )
donde b=base y a=lados iguales
Términos importantes:
1. Mediana: Una línea que une el punto medio de un lado de un triángulo con el vértice opuesto se llama radián.
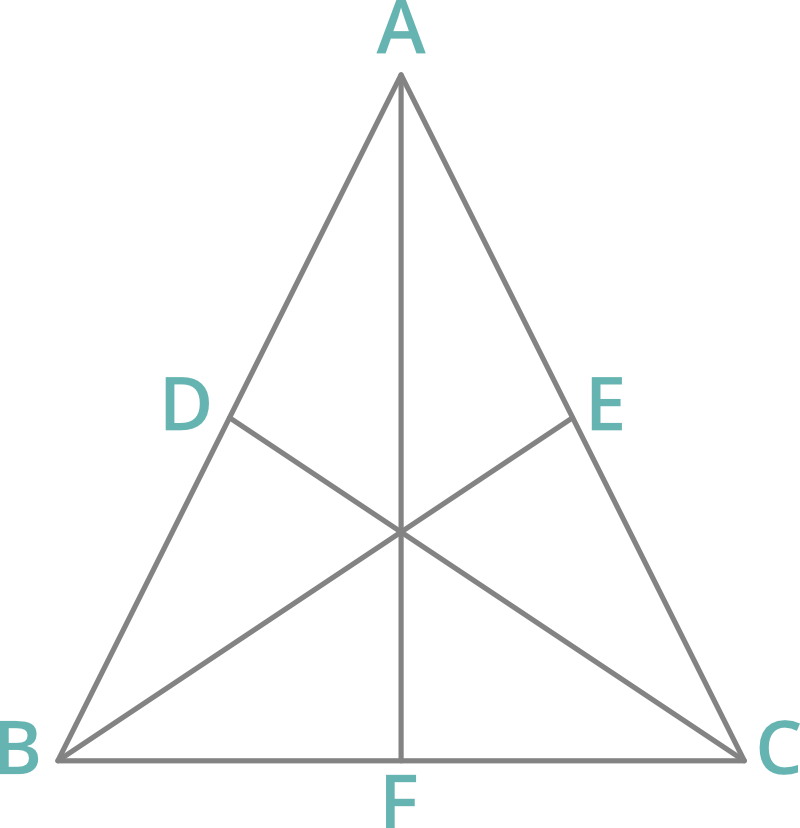
- Una mediana divide un triángulo en dos partes de igual área.
- El punto donde se encuentran las tres medianas se llama baricentro del triángulo.
- El baricentro de un triángulo divide cada mediana en razón 2:1.
2. Altitud: Se llama altitud a la perpendicular trazada desde cualquier vértice hacia el lado opuesto.
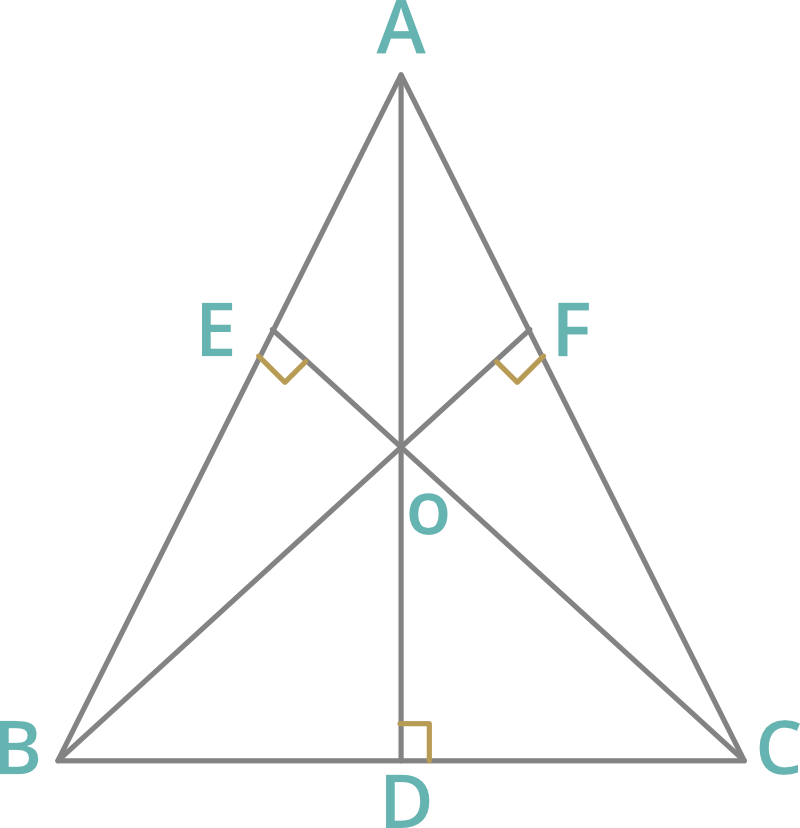
- El punto donde todas las alturas se encuentran en un punto se llama ortocentro del triángulo.
3. Bisectriz perpendicular: Una línea que es perpendicular a un lado y lo biseca es la bisectriz perpendicular del lado.
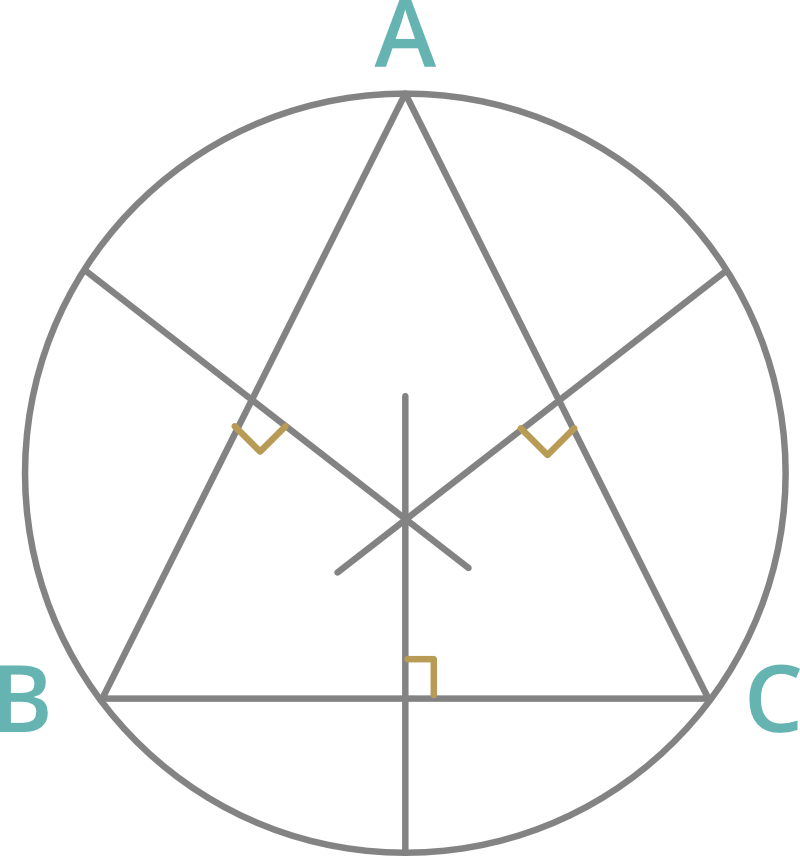
- El punto en el que se unen las mediatrices de los lados se llama circuncentro.
- El circuncentro es el centro de la circunferencia que circunscribe al triángulo.
4. Incentrar:
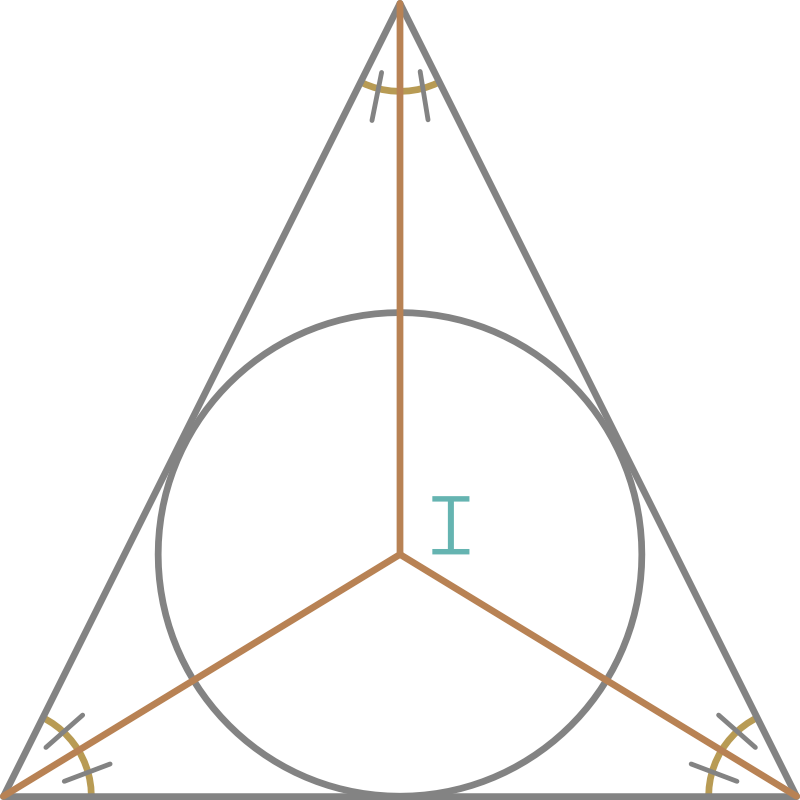
- Las rectas que bisecan los ángulos interiores de un triángulo son las bisectrices de los ángulos de ese triángulo.
- Las bisectrices de los ángulos se encuentran en un punto llamado incentro.
- El ángulo formado por cualquier lado en el incentro es siempre 90° mayor que la mitad del ángulo opuesto al lado.
tangentes:
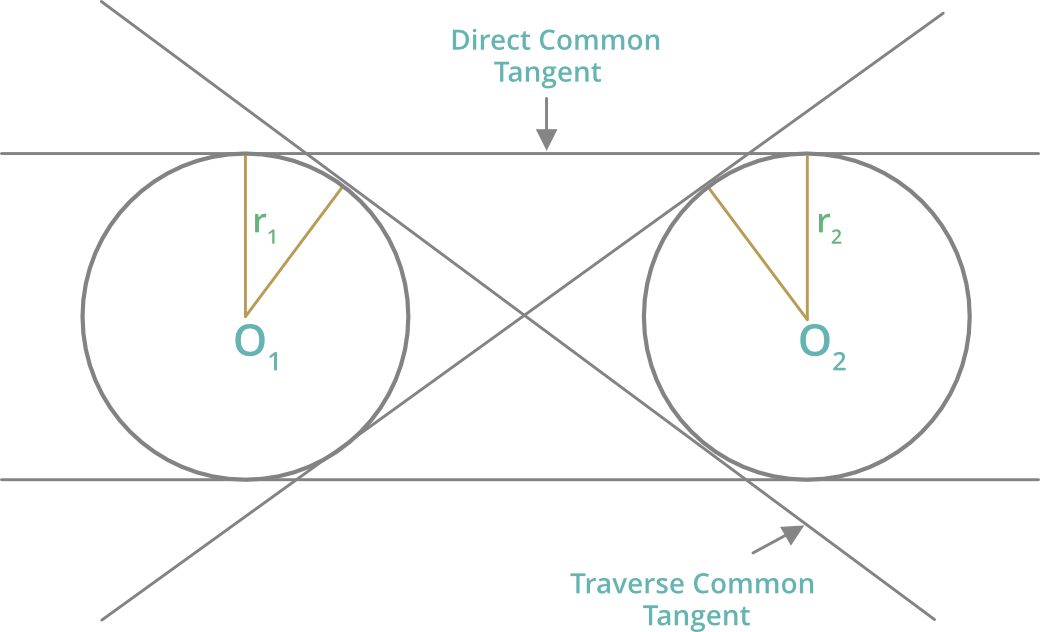
1. La longitud de las tangentes comunes directas es
= √[(Distancia entre sus centros) 2 -(r 1 – r 2 ) 2 ]
= √[(O 1 O 2 ) 2 – (r 1 – r 2 ) 2 ]
2. La longitud de las tangentes comunes transversales es
= √[(Distancia entre sus centros) 2 -(r 1 + r 2 ) 2 ]
= √[(O 1 O 2 ) 2 – (r 1 + r 2 ) 2 ]
Problemas de muestra
Pregunta 1: Si cada ángulo interior de un polígono regular es de 108°. El número de lados del polígono es
Solución: Ángulo interior = 108°
Ángulo exterior = 180 – 108 = 72
Número de lados del polígono = 360° /ángulo exterior
= 360° /72
= 5
Preguntas 2: La razón de los ángulos del triángulo es 2:3:5. Encuentra el ángulo más pequeño del triángulo.
Solución: Relación de ángulos 2:3:5
entonces 2x + 3x + 5x = 180
10x = 180
x = 18
Por lo tanto, el ángulo más pequeño = 18×2 = 36°
Pregunta 3: Dos medianas AD y BE de ∆ABC intersecan a O en ángulo recto. Si AD = 9 cm y BE = 6 cm, entonces la longitud de BD es
Solución:
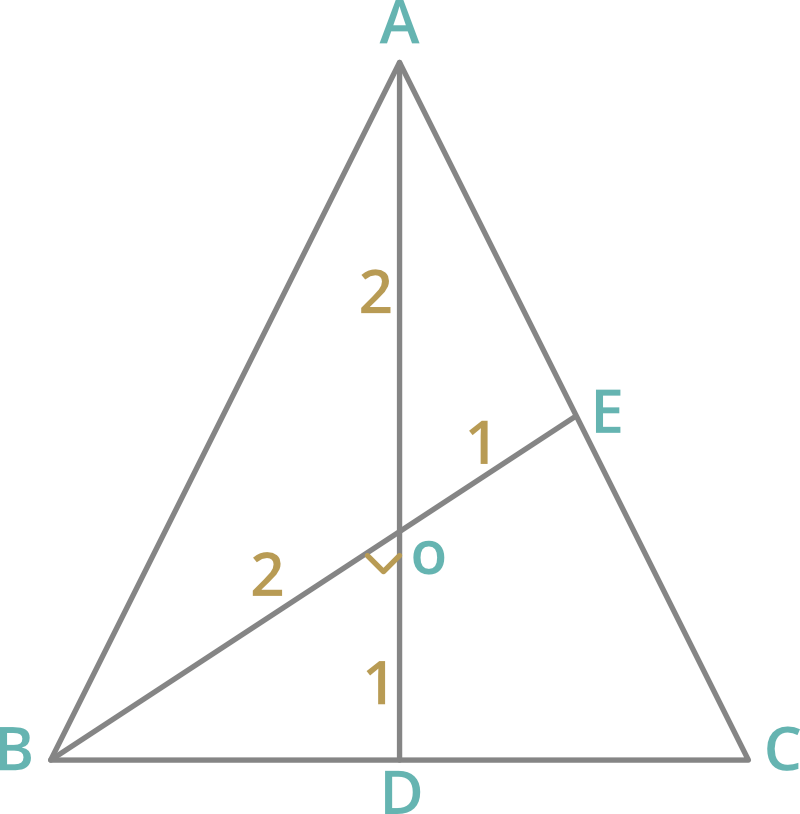
O es el baricentro que divide la mediana en 2:1.
Entonces, AO:OD = 2:1
AD = 3 unidades -> 9 cm
1 unidad -> 3 cm
Entonces, OD = 3 cm
BE = 3 unidades -> 6cm
Entonces, BO = 4 cm
∆BOD es un triángulo rectángulo.
BD 2 = BO 2 + OD 2
BD 2 = (4) 2 + (3) 2
BD 2 = 16 + 9 = 25
BD = 5 cm
Pregunta 4: El lado AB de un paralelogramo ABCD se extiende a E de tal manera que BE = AB, DE interseca a BC en Q. El punto Q divide a BC en la razón
Solución : Acc. preguntar
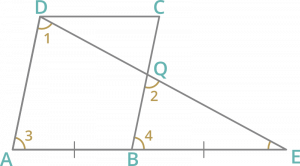
anuncio || BC y AB || DC
∠1 = ∠2 (Ángulo alterno correspondiente)
∠3 = ∠4 (Ángulo alterno correspondiente)
y ∠BEQ es común
Por la propiedad AAA ambos son similares ∆EQB ∼ ∆EDA
Entonces, EB/EA = EQ/ED = QB/AD
AD=BC & EA = 2EB
entonces 1/2 = QB/BC
=> BQ = QC
Por lo tanto, Q divide a BC en razón 1:1.
Pregunta 5: En un ∆ABC, AB=AC y BA se produce a D tal que AC=AD. Entonces el ∠BCD es
Solución: Acc. preguntar
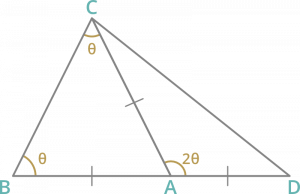
ABC es un triángulo isósceles.
=> ∠C = ∠B = θ
=> ∠CAD = ∠C+ ∠B = 2θ (Un ángulo exterior de un triángulo es igual a la suma de los ángulos interiores opuestos).
AC=AD Entonces, ∆ADC también es un triángulo isósceles.
En ∆CAD, ∠A + ∠C+ ∠D = 180°
2∠C = 180° – 2θ (∠C = ∠D)
∠C = 90° – θ
∠BCD = θ + 90° – θ
∠BCD = 90 °
Pregunta 6: Si O es el circuncentro de ∆PQR, y ∠QOR = 110°, ∠OPR= 25°, entonces el ángulo ∠PRQ es
Solución :
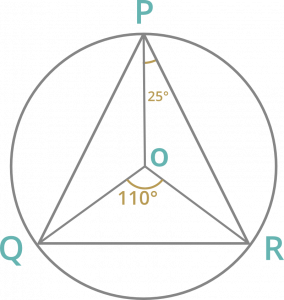
Si O es el circuncentro entonces OP=OR=OQ.
∠OPR = 25°
luego ∠PRO = 25°
In ∆OQR
∠OQR + ∠ORQ + ∠QOR = 180°
2∠ORQ = 180° – 110°
∠ORQ = 35°
Entonces, ∠PRQ = ∠PRO + ∠ORQ
= 25° + 35°
= 60°
Pregunta 7: En ∆ABC, DE || AC, D y E son dos puntos en AB y CB respectivamente. Si AB=20 cm y AD = 8 cm, entonces BE : CE es
Solución :
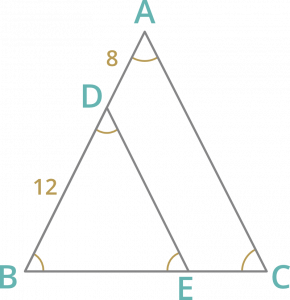
AB = 20 cm y AD = 8 cm
DE || AC
entonces, ∠A = ∠D y ∠C = ∠E
∠B es común
Por propiedad AAA, ∆ABC ∼ ∆DBE por lo
tanto BD/AD = BE/CE
BE/CE = 12/8
BE/CE = 3/2
Por lo tanto , SER : CE = 3:2
Pregunta 8: El ángulo entre las bisectrices internas de dos ángulos de un triángulo ∠B y ∠C es 110°, entonces ∠A es
Solución:
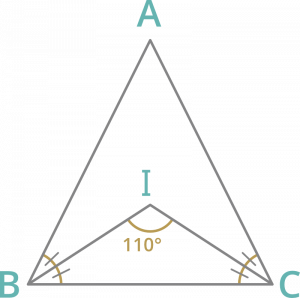
Las bisectrices internas de los ángulos se intersecan en Inccentro.
∠BIC = 110°
El ángulo formado por cualquier lado en el centro es siempre 90° más que la mitad del ángulo opuesto al lado. Entonces,
∠BIC = 90° + 1/2∠A
1/2∠A = 110° – 90°
∠A = 20×2 = 40°
Pregunta 9: La distancia entre dos cuerdas paralelas de 8 cm de longitud y cada una en un círculo de 10 cm de diámetro es
Solución:
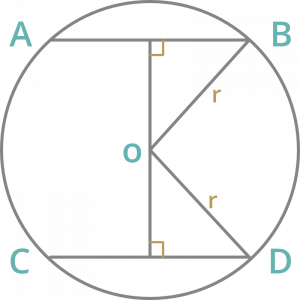
AB = CD = 8 cm de
radio = D/2 = 10/2 = 5 cm
In ∆OMB
OB 2 =OM 2 + MB 2
5 2 = OM 2 + 4 2
OM 2 = 25 – 16
OM = 3 cm
MN = 2 x OM = 2 x 3 = 6 cm
Pregunta 10: El radio de dos círculos concéntricos es de 12 cm y 13 cm. Si la cuerda del círculo mayor es tangente al círculo menor, entonces la longitud de esa cuerda es:
Solución: Acc. preguntar
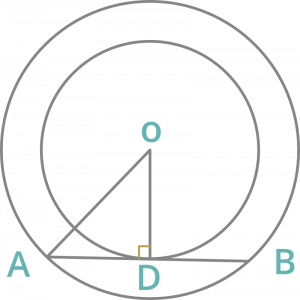
AO = 13 cm y OD = 12 cm
In ∆AOD
AO 2 = DO 2 + AD 2
13 2 = 12 2 + AD 2
AD 2 = 169 – 144
AD = 5 cm
AB = 2xAD = 10 cm
Pregunta 11: Se dibujan dos tangentes en los extremos del diámetro AB de un círculo con centro O. Si una tangente al círculo en el punto C interseca a las otras dos tangentes en Q y R, entonces la medida del ∠QOR es
Solución : Cuenta preguntar
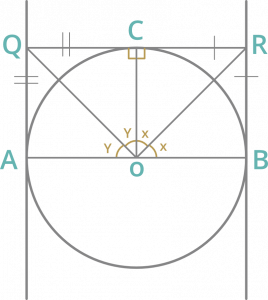
En ∆OCR y ∆RBO
OC = OB (radio)
RC = RB (tangente del mismo punto)
PR es común
Por propiedad SSS ambos son congruentes ∆OCR ≅ ∆RBO Del mismo
modo también son congruentes ∆OCQ ≅ ∆QAO
Entonces ∠COR = ∠ ROB = x
y ∠AOQ = ∠COQ = y
2x + 2y = 180°
x + y = 90°
∠QOR = 90°
Pregunta 12: Dos circunferencias iguales cuyos centros son O y O’ se cortan en el punto A y B, OO’= 24 cm y AB = 10 cm entonces el radio de la circunferencia es
Solución :
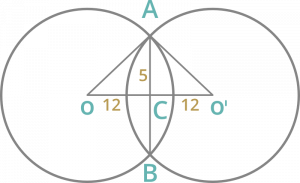
AB = 10 cm
AC = BC = 5 cm
OC = CO’ = 12 cm
En triángulo rectángulo ∆ACO
OA 2 = OC 2 + AC 2
OA 2 = 12 2 + 5 2
OA 2 = 144 + 25
OA = 13 cm
Pregunta 13: La distancia entre los centros de dos círculos de radios 6 cm y 3 cm es de 15 cm. La longitud de la tangente común transversal a los círculos es:
Solución: Longitud de la tangente común transversal = √[(Distancia entre sus centros) 2 -(r 1 + r 2 ) 2 ]
=√[(15) 2 -(6 + 3) 2 ]
=√(225 – 81)
= 12 cm
Pregunta 14: Si la distancia entre dos puntos (0, -5) y (x, 0) es de 13 unidades, entonces el valor de x es:
Solución: Sabemos que
(Distancia) 2 =[(x 2 -x 1 ) 2 + (y 2 – y 1 ) 2 ]
(13) 2 = [(x 2 -0) 2 + (0 – (-5) ) 2 ]
169 = x 2 + 25
x = 12 unidades
Publicación traducida automáticamente
Artículo escrito por Praveenruhil y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA