Un gráfico de etapas múltiples es un gráfico dirigido y ponderado en el que los Nodes se pueden dividir en un conjunto de etapas, de modo que todos los bordes son solo de una etapa a la siguiente etapa (en otras palabras, no hay borde entre los vértices de la misma etapa y de un vértice de la etapa actual a la etapa anterior).
Los vértices de un gráfico multietapa se dividen en n número de subconjuntos disjuntos S = { S 1 , S 2 , S 3 ……….. S n }, donde S 1 es la fuente y S n es el sumidero (destino). La cardinalidad de S 1 y S n es igual a 1, es decir, |S 1 | = | Sn | = 1.
Tenemos un gráfico de etapas múltiples, una fuente y un destino, necesitamos encontrar el camino más corto desde la fuente hasta el destino. Por convención, consideramos el origen en la etapa 1 y el destino en la última etapa.
El siguiente es un gráfico de ejemplo que consideraremos en este artículo:
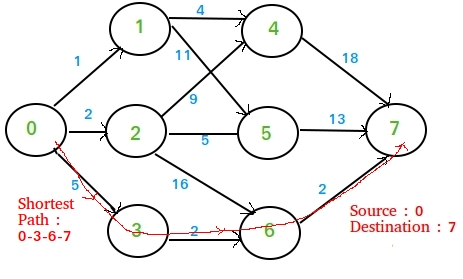
Ahora hay varias estrategias que podemos aplicar: –
- El método de fuerza bruta para encontrar todos los caminos posibles entre el origen y el destino y luego encontrar el mínimo. Esa es la PEOR estrategia posible.
- Algoritmo de Dijkstra de caminos más cortos de fuente única. Este método encontrará las rutas más cortas desde el origen hasta todos los demás Nodes, lo que no es necesario en este caso. Por lo tanto, tomará mucho tiempo y ni siquiera usa la función ESPECIAL que tiene este gráfico MULTI-ETAPA.
- Método codicioso simple : en cada Node, elija la ruta de salida más corta. Si aplicamos este enfoque al gráfico de ejemplo anterior, obtenemos la solución como 1 + 4 + 18 = 23. Pero una mirada rápida al gráfico mostrará caminos disponibles mucho más cortos que 23. ¡Así que el método codicioso falla!
- La mejor opción es la Programación Dinámica. Por lo tanto, debemos encontrar la subestructura óptima, las ecuaciones recursivas y los subproblemas superpuestos.
Subestructura óptima y ecuación recursiva:-
Definimos la notación:- M(x, y) como el costo mínimo para T(Node objetivo) de la Etapa x, Node y.
Shortest distance from stage 1, node 0 to
destination, i.e., 7 is M(1, 0).
// From 0, we can go to 1 or 2 or 3 to
// reach 7.
M(1, 0) = min(1 + M(2, 1),
2 + M(2, 2),
5 + M(2, 3))
Esto significa que nuestro problema de 0 —> 7 ahora se subdivide en 3 subproblemas:
So if we have total 'n' stages and target as T, then the stopping condition will be :- M(n-1, i) = i ---> T + M(n, T) = i ---> T
Árbol de recurrencia y subproblemas superpuestos:-
Entonces, la jerarquía de las evaluaciones M(x, y) se verá así:-
In M(i, j), i is stage number and
j is node number
M(1, 0)
/ | \
/ | \
M(2, 1) M(2, 2) M(2, 3)
/ \ / \ / \
M(3, 4) M(3, 5) M(3, 4) M(3, 5) M(3, 6) M(3, 6)
. . . . . .
. . . . . .
. . . . . .
Entonces, aquí hemos dibujado una parte muy pequeña del árbol de recurrencia y ya podemos ver los subproblemas superpuestos. Podemos reducir en gran medida el número de evaluaciones M(x, y) utilizando la programación dinámica.
Detalles de la implementación:
La siguiente implementación asume que los Nodes están numerados de 0 a N-1 desde la primera etapa (origen) hasta la última etapa (destino). También asumimos que el gráfico de entrada es multietapa.
Usamos el enfoque de arriba a abajo y usamos la array dist[] para almacenar el valor del subproblema superpuesto.
dist[i] almacenará el valor de la distancia mínima desde el Node i hasta el Node n-1 (Node de destino).
Por lo tanto, dist[0] almacenará la distancia mínima entre el Node de origen y el Node de destino.
C++
// CPP program to find shortest distance
// in a multistage graph.
#include<bits/stdc++.h>
using namespace std;
#define N 8
#define INF INT_MAX
// Returns shortest distance from 0 to
// N-1.
int shortestDist(int graph[N][N]) {
// dist[i] is going to store shortest
// distance from node i to node N-1.
int dist[N];
dist[N-1] = 0;
// Calculating shortest path for
// rest of the nodes
for (int i = N-2 ; i >= 0 ; i--)
{
// Initialize distance from i to
// destination (N-1)
dist[i] = INF;
// Check all nodes of next stages
// to find shortest distance from
// i to N-1.
for (int j = i ; j < N ; j++)
{
// Reject if no edge exists
if (graph[i][j] == INF)
continue;
// We apply recursive equation to
// distance to target through j.
// and compare with minimum distance
// so far.
dist[i] = min(dist[i], graph[i][j] +
dist[j]);
}
}
return dist[0];
}
// Driver code
int main()
{
// Graph stored in the form of an
// adjacency Matrix
int graph[N][N] =
{{INF, 1, 2, 5, INF, INF, INF, INF},
{INF, INF, INF, INF, 4, 11, INF, INF},
{INF, INF, INF, INF, 9, 5, 16, INF},
{INF, INF, INF, INF, INF, INF, 2, INF},
{INF, INF, INF, INF, INF, INF, INF, 18},
{INF, INF, INF, INF, INF, INF, INF, 13},
{INF, INF, INF, INF, INF, INF, INF, 2},
{INF, INF, INF, INF, INF, INF, INF, INF}};
cout << shortestDist(graph);
return 0;
}
Java
// Java program to find shortest distance
// in a multistage graph.
class GFG
{
static int N = 8;
static int INF = Integer.MAX_VALUE;
// Returns shortest distance from 0 to
// N-1.
public static int shortestDist(int[][] graph)
{
// dist[i] is going to store shortest
// distance from node i to node N-1.
int[] dist = new int[N];
dist[N - 1] = 0;
// Calculating shortest path for
// rest of the nodes
for (int i = N - 2; i >= 0; i--)
{
// Initialize distance from i to
// destination (N-1)
dist[i] = INF;
// Check all nodes of next stages
// to find shortest distance from
// i to N-1.
for (int j = i; j < N; j++)
{
// Reject if no edge exists
if (graph[i][j] == INF)
{
continue;
}
// We apply recursive equation to
// distance to target through j.
// and compare with minimum distance
// so far.
dist[i] = Math.min(dist[i], graph[i][j]
+ dist[j]);
}
}
return dist[0];
}
// Driver code
public static void main(String[] args)
{
// Graph stored in the form of an
// adjacency Matrix
int[][] graph = new int[][]{{INF, 1, 2, 5, INF, INF, INF, INF},
{INF, INF, INF, INF, 4, 11, INF, INF},
{INF, INF, INF, INF, 9, 5, 16, INF},
{INF, INF, INF, INF, INF, INF, 2, INF},
{INF, INF, INF, INF, INF, INF, INF, 18},
{INF, INF, INF, INF, INF, INF, INF, 13},
{INF, INF, INF, INF, INF, INF, INF, 2}};
System.out.println(shortestDist(graph));
}
}
// This code has been contributed by 29AjayKumar
Python3
# Python3 program to find shortest # distance in a multistage graph. # Returns shortest distance from # 0 to N-1. def shortestDist(graph): global INF # dist[i] is going to store shortest # distance from node i to node N-1. dist = [0] * N dist[N - 1] = 0 # Calculating shortest path # for rest of the nodes for i in range(N - 2, -1, -1): # Initialize distance from # i to destination (N-1) dist[i] = INF # Check all nodes of next stages # to find shortest distance from # i to N-1. for j in range(N): # Reject if no edge exists if graph[i][j] == INF: continue # We apply recursive equation to # distance to target through j. # and compare with minimum # distance so far. dist[i] = min(dist[i], graph[i][j] + dist[j]) return dist[0] # Driver code N = 8 INF = 999999999999 # Graph stored in the form of an # adjacency Matrix graph = [[INF, 1, 2, 5, INF, INF, INF, INF], [INF, INF, INF, INF, 4, 11, INF, INF], [INF, INF, INF, INF, 9, 5, 16, INF], [INF, INF, INF, INF, INF, INF, 2, INF], [INF, INF, INF, INF, INF, INF, INF, 18], [INF, INF, INF, INF, INF, INF, INF, 13], [INF, INF, INF, INF, INF, INF, INF, 2]] print(shortestDist(graph)) # This code is contributed by PranchalK
C#
// C# program to find shortest distance
// in a multistage graph.
using System;
class GFG
{
static int N = 8;
static int INF = int.MaxValue;
// Returns shortest distance from 0 to
// N-1.
public static int shortestDist(int[,] graph) {
// dist[i] is going to store shortest
// distance from node i to node N-1.
int[] dist = new int[N];
dist[N-1] = 0;
// Calculating shortest path for
// rest of the nodes
for (int i = N-2 ; i >= 0 ; i--)
{
// Initialize distance from i to
// destination (N-1)
dist[i] = INF;
// Check all nodes of next stages
// to find shortest distance from
// i to N-1.
for (int j = i ; j < N ; j++)
{
// Reject if no edge exists
if (graph[i,j] == INF)
continue;
// We apply recursive equation to
// distance to target through j.
// and compare with minimum distance
// so far.
dist[i] = Math.Min(dist[i], graph[i,j] +
dist[j]);
}
}
return dist[0];
}
// Driver code
static void Main()
{
// Graph stored in the form of an
// adjacency Matrix
int[,] graph = new int[,]
{{INF, 1, 2, 5, INF, INF, INF, INF},
{INF, INF, INF, INF, 4, 11, INF, INF},
{INF, INF, INF, INF, 9, 5, 16, INF},
{INF, INF, INF, INF, INF, INF, 2, INF},
{INF, INF, INF, INF, INF, INF, INF, 18},
{INF, INF, INF, INF, INF, INF, INF, 13},
{INF, INF, INF, INF, INF, INF, INF, 2}};
Console.Write(shortestDist(graph));
}
}
// This code is contributed by DrRoot_
Javascript
<script>
// JavaScript program to find shortest distance
// in a multistage graph.
let N = 8;
let INF = Number.MAX_VALUE;
// Returns shortest distance from 0 to
// N-1.
function shortestDist(graph)
{
// dist[i] is going to store shortest
// distance from node i to node N-1.
let dist = new Array(N);
dist[N - 1] = 0;
// Calculating shortest path for
// rest of the nodes
for (let i = N - 2; i >= 0; i--)
{
// Initialize distance from i to
// destination (N-1)
dist[i] = INF;
// Check all nodes of next stages
// to find shortest distance from
// i to N-1.
for (let j = i; j < N; j++)
{
// Reject if no edge exists
if (graph[i][j] == INF)
{
continue;
}
// We apply recursive equation to
// distance to target through j.
// and compare with minimum distance
// so far.
dist[i] = Math.min(dist[i], graph[i][j]
+ dist[j]);
}
}
return dist[0];
}
let graph = [[INF, 1, 2, 5, INF, INF, INF, INF],
[INF, INF, INF, INF, 4, 11, INF, INF],
[INF, INF, INF, INF, 9, 5, 16, INF],
[INF, INF, INF, INF, INF, INF, 2, INF],
[INF, INF, INF, INF, INF, INF, INF, 18],
[INF, INF, INF, INF, INF, INF, INF, 13],
[INF, INF, INF, INF, INF, INF, INF, 2]];
document.write(shortestDist(graph));
// This code is contributed by rag2127
</script>
9
Complejidad del tiempo : O(n 2 )
Publicación traducida automáticamente
Artículo escrito por Siddhant-Bajaj y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA