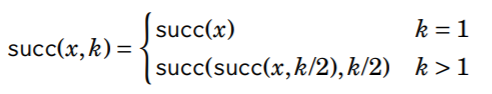Un grafo sucesor es un grafo dirigido en el que cada vértice tiene un grado superior a uno, es decir, exactamente un borde comienza en cada Node. Un grafo sucesor consta de uno o más componentes, cada uno de los cuales contiene un ciclo y algunos caminos que conducen a él.
Los gráficos sucesores a veces se denominan gráficos funcionales . La razón de esto es que cualquier gráfico sucesor corresponde a una función que define los bordes del gráfico. El parámetro de la función es un Node del gráfico y la función da el sucesor de ese Node. Por ejemplo, la función
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| éxito( x ) | 3 | 5 | 7 | 6 | 2 | 2 | 1 | 6 | 3 |
La función anterior define el siguiente gráfico:
Dado que cada Node de un gráfico sucesor tiene un sucesor único, también se puede definir una función succ(x, k) que da el Node cuando un recorrido comienza en el Node x y camina k pasos hacia adelante. Por ejemplo, en el gráfico anterior succ(4, 6) = 2 , porque se puede llegar al Node 2 caminando 6 pasos desde el Node 4 :
Una forma sencilla de calcular un valor de succ( x, k ) es comenzar en el Node x y caminar k pasos hacia adelante, lo que lleva O(k) tiempo. Sin embargo, usando preprocesamiento, cualquier valor de succ( x, k ) puede calcularse solo en tiempo O(logk) .
La idea es precalcular todos los valores de succ( x, k ) donde k es una potencia de dos y como máximo u , donde u es el número máximo de pasos que caminaremos. Esto se puede hacer de manera eficiente porque podemos usar la siguiente recursividad:
Precalcular los valores lleva tiempo O(n*log u) porque los valores O(log u) se calculan para cada Node. En el gráfico anterior, los primeros valores son los siguientes:
| X | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| éxito( x , 1) | 3 | 5 | 7 | 6 | 2 | 2 | 1 | 6 | 3 |
| éxito( x , 2) | 7 | 2 | 1 | 2 | 5 | 5 | 3 | 2 | 7 |
| éxito( x , 4) | 3 | 2 | 7 | 2 | 5 | 5 | 1 | 2 | 3 |
| éxito( x , 8) | 7 | 2 | 1 | 2 | 5 | 5 | 3 | 2 | 7 |
| … |
Después de esto, cualquier valor de succ( x, k ) se puede calcular presentando el número de pasos k como una suma de potencias de dos.
Por ejemplo, si queremos calcular el valor de succ(x, 11) , primero formamos la representación 11 = 8 + 2 + 1. Usando eso
![]()
Por ejemplo, en el gráfico anterior
![]()
Tal representación siempre consta de O(log k) partes, por lo que calcular un valor de succ( x, k ) lleva O(log k) tiempo.
Publicación traducida automáticamente
Artículo escrito por mohdkhubaibmhps y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA