Gráficos de superficie y gráficos de contorno en Python

Matplotlib se introdujo teniendo en cuenta, solo el trazado bidimensional. Pero en el momento en que se produjo el lanzamiento de 1.0, las utilidades 3D se desarrollaron sobre la 2D y, por lo tanto, ¡tenemos una implementación de datos 3D disponible hoy! Los gráficos en 3D se habilitan al importar el kit de herramientas mplot3d. En este artículo, discutiremos los gráficos de superficie y los gráficos de contorno en detalle.

Parcelas de superficie

Un gráfico de superficie es una representación de un conjunto de datos tridimensional. Describe una relación funcional entre dos variables independientes X y Z y una variable dependiente designada Y, en lugar de mostrar los puntos de datos individuales. Es una gráfica complementaria de la gráfica de contorno. Es similar al diagrama de estructura alámbrica, pero cada cara de la estructura alámbrica es un polígono relleno. Esto ayuda a crear la topología de la superficie que se está visualizando.

Los gráficos de superficie se utilizan para:

• Visualice las funciones de pérdida en el aprendizaje automático y el aprendizaje profundo
• Visualice las funciones de valor de almacenamiento o estado en el aprendizaje por refuerzo

Creación de un gráfico de superficie 3D

El axes3d presente en el kit de herramientas mpl_toolkits.mplot3d de Matplotlib proporciona las funciones necesarias para crear gráficos de superficie 3D. Los gráficos de superficie se crean mediante el uso de ax.plot_surface()la función.

Sintaxis:

ax.plot_surface(X, Y, Z)

donde X e Y son arrays 2D de puntos de x e y, mientras que Z es una array 2D de alturas.

Ejemplo 1:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
  
a = np.array([1, 2, 3])
b = np.array([4, 5, 6, 7])
  
a, b = np.meshgrid(a, b)
  
# surface plot for a + b
fig = plt.figure()
axes = fig.gca(projection ='3d')
axes.plot_surface(a, b, a + b)
  
plt.show()

Producción:

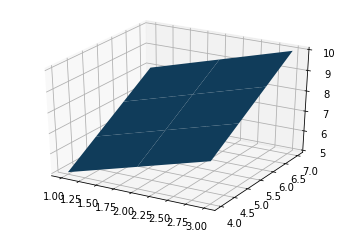
Ejemplo 2:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
  
a = np.array([1, 2, 3])
b = np.array([4, 5, 6, 7])
  
a, b = np.meshgrid(a, b)
  
# surface plot for a**2 + b**2
a = np.arange(-1, 1, 0.02)
b = a
a, b = np.meshgrid(a, b)
  
fig = plt.figure()
axes = fig.gca(projection ='3d')
axes.plot_surface(a, b, a**2 + b**2)
  
plt.show()

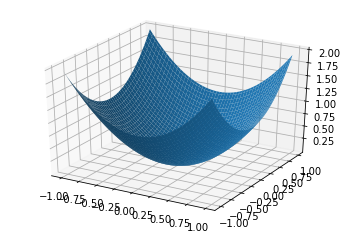
Gráficos de contorno

Los gráficos de contorno, también llamados gráficos de nivel, son una herramienta para realizar análisis multivariados y visualizar gráficos 3D en un espacio 2D. Si consideramos X e Y como nuestras variables que queremos graficar, entonces la respuesta Z se graficará como cortes en el plano XY debido a que los contornos a veces se denominan cortes Z o isorrespuesta.

Los gráficos de contorno se utilizan ampliamente para visualizar la densidad, las altitudes o las alturas de la montaña, así como en el departamento meteorológico. Debido a su uso tan amplio, matplotlib.pyplotproporciona un contorno de método para que nos sea más fácil dibujar gráficos de contorno.

Creación de gráficos de contorno

Matplotlib.pyplot.contour() suele ser útil cuando Z = f(X, Y), es decir, Z cambia en función de las entradas X e Y. También está disponible un contourf() que nos permite dibujar contornos rellenos.

Sintaxis:

matplotlib.pyplot.contour([X, Y, ] Z, [levels], **kwargs)

dónde,

• X, Y: arrays NumPy 2-D con la misma forma que Z o arrays 1-D tales que len(X)==My len(Y)==N(donde M y N son filas y columnas de Z)
  Z: los valores de altura sobre los que se dibuja el contorno. La forma es (M, N)
  niveles: determina el número y las posiciones de las líneas/regiones de contorno.

Ejemplo 1:

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
  
a = np.array([1, 2, 3])
b = np.array([4, 5, 6, 7])
  
a, b = np.meshgrid(a, b)
  
# surface plot for a + b
fig = plt.figure()
axes = fig.gca(projection ='3d')
axes.contour(a, b, a + b)
  
plt.show()

Producción:

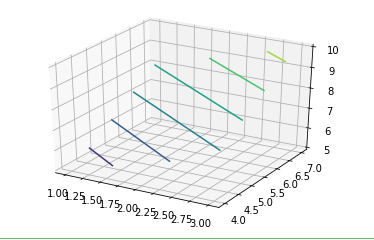
Ejemplo 2:

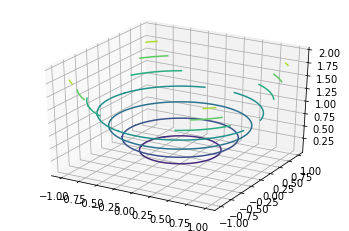
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
  
a = np.array([1, 2, 3])
b = np.array([4, 5, 6, 7])
  
a, b = np.meshgrid(a, b)
  
# surface plot for a**2 + b**2
a = np.arange(-1, 1, 0.02)
b = a
a, b = np.meshgrid(a, b)
  
fig = plt.figure()
axes = fig.gca(projection ='3d')
axes.contour(a, b, a**2 + b**2)
  
plt.show()

Producción: