Prerrequisito: técnica de visualización básica para un gráfico
En el artículo anterior , hemos aprendido sobre los conceptos básicos del módulo Networkx y cómo crear un gráfico no dirigido. Tenga en cuenta que el módulo Networkx genera fácilmente los diversos parámetros gráficos, como se muestra a continuación con un ejemplo.
import networkx as nx
edges = [(1, 2), (1, 6), (2, 3), (2, 4), (2, 6),
(3, 4), (3, 5), (4, 8), (4, 9), (6, 7)]
G.add_edges_from(edges)
nx.draw_networkx(G, with_label = True)
print("Total number of nodes: ", int(G.number_of_nodes()))
print("Total number of edges: ", int(G.number_of_edges()))
print("List of all nodes: ", list(G.nodes()))
print("List of all edges: ", list(G.edges(data = True)))
print("Degree for all nodes: ", dict(G.degree()))
print("Total number of self-loops: ", int(G.number_of_selfloops()))
print("List of all nodes with self-loops: ",
list(G.nodes_with_selfloops()))
print("List of all nodes we can go to in a single step from node 2: ",
list(G.neighbors(2)))
Producción: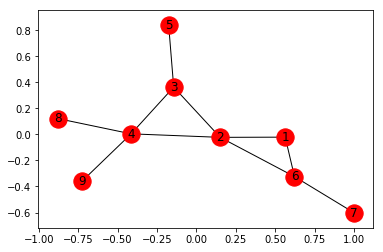
Número total de Nodes: 9
Número total de aristas: 10
Lista de todos los Nodes: [1, 2, 3, 4, 5, 6, 7, 8, 9]
Lista de todas las aristas: [(1, 2, {}) , (1, 6, {}), (2, 3, {}), (2, 4, {}), (2, 6, {}), (3, 4, {}), (3, 5 , {}), (4, 8, {}), (4, 9, {}), (6, 7, {})]
Grado para todos los Nodes: {1: 2, 2: 4, 3: 3, 4: 4, 5: 1, 6: 3, 7: 1, 8: 1, 9: 1}
Número total de bucles automáticos: 0
Lista de todos los Nodes con bucles automáticos: []
Lista de todos los Nodes a los que podemos ir en un solo paso desde el Node 2: [1, 3, 4, 6]
Creación de un gráfico no dirigido ponderado –
Agregue una lista de todos los bordes junto con una variedad de pesos:
import networkx as nx G = nx.Graph() edges = [(1, 2, 19), (1, 6, 15), (2, 3, 6), (2, 4, 10), (2, 6, 22), (3, 4, 51), (3, 5, 14), (4, 8, 20), (4, 9, 42), (6, 7, 30)] G.add_weighted_edges_from(edges) nx.draw_networkx(G, with_labels = True)
Podemos agregar los bordes a través de una Lista de bordes, que debe guardarse en un .txtformato (por ejemplo, edge_list.txt)
G = nx.read_edgelist('edge_list.txt', data =[('Weight', int)])
1 2 19 1 6 15 2 3 6 2 4 10 2 6 22 3 4 51 3 5 14 4 8 20 4 9 42 6 7 30
La lista de bordes también se puede leer a través de un marco de datos de Pandas:
import pandas as pd
df = pd.read_csv('edge_list.txt', delim_whitespace = True,
header = None, names =['n1', 'n2', 'weight'])
G = nx.from_pandas_dataframe(df, 'n1', 'n2', edge_attr ='weight')
# The Graph diagram does not show the edge weights.
# However, we can get the weights by printing all the
# edges along with the weights by the command below
print(list(G.edges(data = True)))
Producción:
[(1, 2, {'weight': 19}),
(1, 6, {'weight': 15}),
(2, 3, {'weight': 6}),
(2, 4, {'weight': 10}),
(2, 6, {'weight': 22}),
(3, 4, {'weight': 51}),
(3, 5, {'weight': 14}),
(4, 8, {'weight': 20}),
(4, 9, {'weight': 42}),
(6, 7, {'weight': 30})]
Ahora exploraríamos las diferentes técnicas de visualización de un gráfico.
Para esto, creamos un conjunto de datos de varias ciudades indias y las distancias entre ellas y lo guardamos en un .txtarchivo, edge_list.txt.
Kolkata Mumbai 2031 Mumbai Pune 155 Mumbai Goa 571 Kolkata Delhi 1492 Kolkata Bhubaneshwar 444 Mumbai Delhi 1424 Delhi Chandigarh 243 Delhi Surat 1208 Kolkata Hyderabad 1495 Hyderabad Chennai 626 Chennai Thiruvananthapuram 773 Thiruvananthapuram Hyderabad 1299 Kolkata Varanasi 679 Delhi Varanasi 821 Mumbai Bangalore 984 Chennai Bangalore 347 Hyderabad Bangalore 575 Kolkata Guwahati 1031
Ahora, haremos un gráfico con el siguiente código. También agregaremos un atributo de Node a todas las ciudades que será la población de cada ciudad.
import networkx as nx
G = nx.read_weighted_edgelist('edge_list.txt', delimiter =" ")
population = {
'Kolkata' : 4486679,
'Delhi' : 11007835,
'Mumbai' : 12442373,
'Guwahati' : 957352,
'Bangalore' : 8436675,
'Pune' : 3124458,
'Hyderabad' : 6809970,
'Chennai' : 4681087,
'Thiruvananthapuram' : 460468,
'Bhubaneshwar' : 837737,
'Varanasi' : 1198491,
'Surat' : 4467797,
'Goa' : 40017,
'Chandigarh' : 961587
}
# We have to set the population attribute for each of the 14 nodes
for i in list(G.nodes()):
G.nodes[i]['population'] = population[i]
nx.draw_networkx(G, with_label = True)
# This line allows us to visualize the Graph
Producción: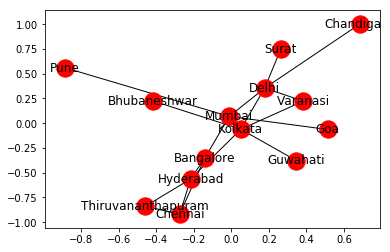
Pero podemos personalizar la Red para proporcionar más información visualmente siguiendo estos pasos:
- El tamaño del Node es proporcional a la población de la ciudad.
- La intensidad del color del Node es directamente proporcional al grado del Node.
- El ancho del borde es directamente proporcional al peso del borde, en este caso, la distancia entre las ciudades.
# fixing the size of the figure
plt.figure(figsize =(10, 7))
node_color = [G.degree(v) for v in G]
# node colour is a list of degrees of nodes
node_size = [0.0005 * nx.get_node_attributes(G, 'population')[v] for v in G]
# size of node is a list of population of cities
edge_width = [0.0015 * G[u][v]['weight'] for u, v in G.edges()]
# width of edge is a list of weight of edges
nx.draw_networkx(G, node_size = node_size,
node_color = node_color, alpha = 0.7,
with_labels = True, width = edge_width,
edge_color ='.4', cmap = plt.cm.Blues)
plt.axis('off')
plt.tight_layout();
Producción: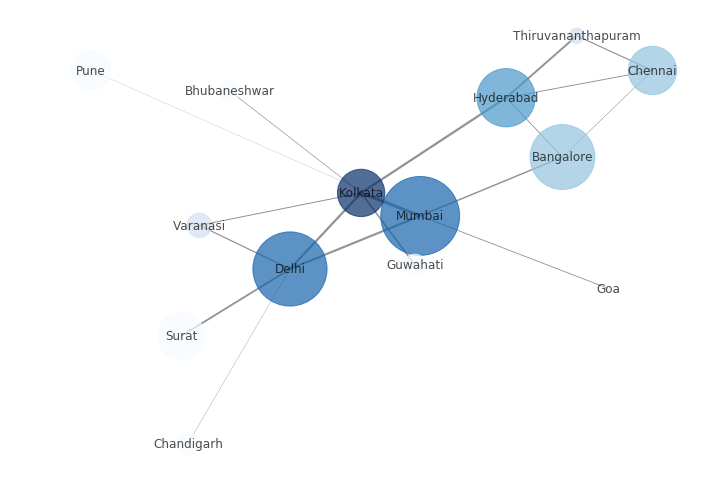
Podemos ver en el código anterior que hemos especificado el tipo de diseño como apretado. Puede encontrar las diferentes técnicas de diseño y probar algunas de ellas como se muestra en el siguiente código:
print("The various layout options are:")
print([x for x in nx.__dir__() if x.endswith('_layout')])
# prints out list of all different layout options
node_color = [G.degree(v) for v in G]
node_size = [0.0005 * nx.get_node_attributes(G, 'population')[v] for v in G]
edge_width = [0.0015 * G[u][v]['weight'] for u, v in G.edges()]
plt.figure(figsize =(10, 9))
pos = nx.random_layout(G)
print("Random Layout:")
# demonstrating random layout
nx.draw_networkx(G, pos, node_size = node_size,
node_color = node_color, alpha = 0.7,
with_labels = True, width = edge_width,
edge_color ='.4', cmap = plt.cm.Blues)
plt.figure(figsize =(10, 9))
pos = nx.circular_layout(G)
print("Circular Layout")
# demonstrating circular layout
nx.draw_networkx(G, pos, node_size = node_size,
node_color = node_color, alpha = 0.7,
with_labels = True, width = edge_width,
edge_color ='.4', cmap = plt.cm.Blues)
Producción:
The various layout options are: ['rescale_layout', 'random_layout', 'shell_layout', 'fruchterman_reingold_layout', 'spectral_layout', 'kamada_kawai_layout', 'spring_layout', 'circular_layout'] Random Layout:Circular Layout:

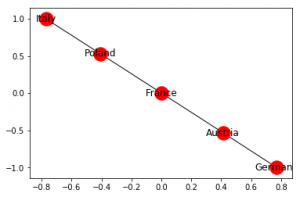
Networkx nos permite crear un Path Graph, es decir, una línea recta que conecta varios Nodes de la siguiente manera:
G2 = nx.path_graph(5) nx.draw_networkx(G2, with_labels = True)
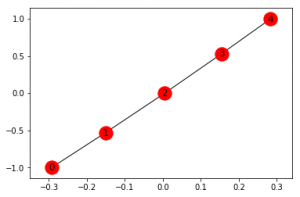
Podemos cambiar el nombre de los Nodes –
G2 = nx.path_graph(5)
new = {0:"Germany", 1:"Austria", 2:"France", 3:"Poland", 4:"Italy"}
G2 = nx.relabel_nodes(G2, new)
nx.draw_networkx(G2, with_labels = True)
Creación de gráficos dirigidos –
Networkx nos permite trabajar con Grafos Dirigidos. Su creación, la adición de Nodes, bordes, etc. son exactamente similares a los de un gráfico no dirigido como se explica aquí .
El siguiente código muestra las operaciones básicas en un gráfico dirigido.
import networkx as nx
G = nx.DiGraph()
G.add_edges_from([(1, 1), (1, 7), (2, 1), (2, 2), (2, 3),
(2, 6), (3, 5), (4, 3), (5, 4), (5, 8),
(5, 9), (6, 4), (7, 2), (7, 6), (8, 7)])
plt.figure(figsize =(9, 9))
nx.draw_networkx(G, with_label = True, node_color ='green')
# getting different graph attributes
print("Total number of nodes: ", int(G.number_of_nodes()))
print("Total number of edges: ", int(G.number_of_edges()))
print("List of all nodes: ", list(G.nodes()))
print("List of all edges: ", list(G.edges()))
print("In-degree for all nodes: ", dict(G.in_degree()))
print("Out degree for all nodes: ", dict(G.out_degree))
print("Total number of self-loops: ", int(G.number_of_selfloops()))
print("List of all nodes with self-loops: ",
list(G.nodes_with_selfloops()))
print("List of all nodes we can go to in a single step from node 2: ",
list(G.successors(2)))
print("List of all nodes from which we can go to node 2 in a single step: ",
list(G.predecessors(2)))
Producción: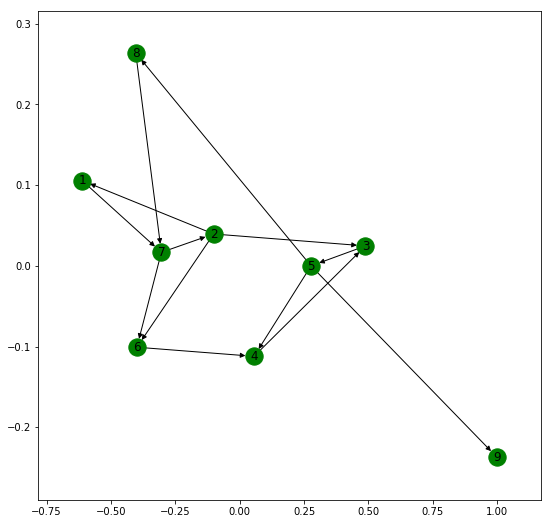
Número total de Nodes: 9
Número total de aristas: 15
Lista de todos los Nodes: [1, 2, 3, 4, 5, 6, 7, 8, 9]
Lista de todas las aristas: [(1, 1), (1 , 7), (2, 1), (2, 2), (2, 3), (2, 6), (3, 5), (4, 3), (5, 8), (5, 9 ), (5, 4), (6, 4), (7, 2), (7, 6), (8, 7)]
Grado de entrada para todos los Nodes: {1: 2, 2: 2, 3: 2, 4: 2, 5: 1, 6: 2, 7: 2, 8: 1, 9: 1}
Grado de salida para todos los Nodes: {1: 2, 2: 4, 3: 1, 4: 1, 5 : 3, 6: 1, 7: 2, 8: 1, 9: 0}
Número total de bucles automáticos: 2
Lista de todos los Nodes con bucles automáticos: [1, 2]
Lista de todos los Nodes a los que podemos ir en un solo paso desde el Node 2: [1, 2, 3, 6]
Lista de todos los Nodes desde los que podemos ir al Node 2 en un solo paso: [2, 7]
Ahora, mostraremos las operaciones básicas para un MultiGraph. Networkx nos permite crear Multigraphs dirigidos y no dirigidos. Un Multigraph es un Graph donde múltiples bordes paralelos pueden conectar los mismos Nodes.
Por ejemplo, creemos una red de 10 personas, A, B, C, D, E, F, G, H, I y J. Tienen cuatro relaciones diferentes entre ellos, a saber, Amigo, Compañero de trabajo, Familia y Vecino. Una relación entre dos personas no se restringe a un solo tipo.
Pero la visualización de Multigraph en Networkx no está clara. No muestra varios bordes por separado y estos bordes se superponen.
import networkx as nx
import matplotlib.pyplot as plt
G = nx.MultiGraph()
relations = [('A', 'B', 'neighbour'), ('A', 'B', 'friend'), ('B', 'C', 'coworker'),
('C', 'F', 'coworker'), ('C', 'F', 'friend'), ('F', 'G', 'coworker'),
('F', 'G', 'family'), ('C', 'E', 'friend'), ('E', 'D', 'family'),
('E', 'I', 'coworker'), ('E', 'I', 'neighbour'), ('I', 'J', 'coworker'),
('E', 'J', 'friend'), ('E', 'H', 'coworker')]
for i in relations:
G.add_edge(i[0], i[1], relation = i[2])
plt.figure(figsize =(9, 9))
nx.draw_networkx(G, with_label = True)
# getting various graph properties
print("Total number of nodes: ", int(G.number_of_nodes()))
print("Total number of edges: ", int(G.number_of_edges()))
print("List of all nodes: ", list(G.nodes()))
print("List of all edges: ", list(G.edges(data = True)))
print("Degree for all nodes: ", dict(G.degree()))
print("Total number of self-loops: ", int(G.number_of_selfloops()))
print("List of all nodes with self-loops: ", list(G.nodes_with_selfloops()))
print("List of all nodes we can go to in a single step from node E: ",
list(G.neighbors('E")))
Producción: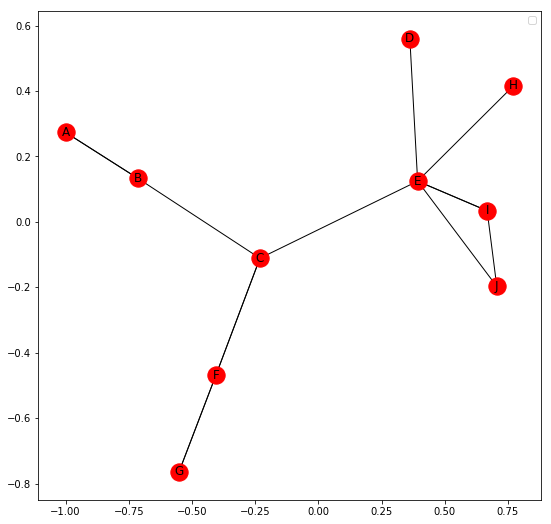
Número total de Nodes: 10
Número total de aristas: 14
Lista de todos los Nodes: [‘E’, ‘I’, ‘D’, ‘B’, ‘C’, ‘F’, ‘H’, ‘A’, ‘J’, ‘G’]
Lista de todas las aristas: [(‘E’, ‘I’, {‘relación’: ‘compañero de trabajo’}), (‘E’, ‘I’, {‘relación’: ‘vecino ‘}), (‘E’, ‘H’, {‘relación’: ‘compañero de trabajo’}), (‘E’, ‘J’, {‘relación’: ‘amigo’}), (‘E’, ‘ C’, {‘relación’: ‘amigo’}), (‘E’, ‘D’, {‘relación’: ‘familia’}), (‘I’, ‘J’, {‘relación’: ‘compañero de trabajo ‘}), (‘B’, ‘A’, {‘relación’: ‘vecino’}), (‘B’, ‘A’, {‘relación’: ‘amigo’}), (‘B’, ‘ C’, {‘relación’: ‘compañero de trabajo’}), (‘C’, ‘F’, {‘relación’: ‘compañero de trabajo’}), (‘C’, ‘F’, {‘relación’: ‘amigo ‘}), (‘F’, ‘G’, {‘relación’: ‘compañero de trabajo’}), (‘F’, ‘G’, {‘relación’: ‘familia’})]
Grado para todos los Nodes: { ‘E’: 6, ‘I’: 3, ‘B’: 3, ‘D’: 1, ‘F’: 4, ‘A’: 2, ‘G’: 2, ‘H’: 1, ‘J ‘: 2, ‘C’: 4}
Número total de bucles automáticos: 0
Lista de todos los Nodes con bucles automáticos: []
Lista de todos los Nodes a los que podemos ir en un solo paso desde el Node E: [‘I’, ‘H’, ‘J’, ‘C ‘, ‘D’]
De manera similar, se puede crear un gráfico multidirigido usando
G = nx.MultiDiGraph()
Publicación traducida automáticamente
Artículo escrito por ArijitGayen y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA