Gráficos L y lo que representan en TOC – Part 1

Requisito previo: introducción a los autómatas finitos
Todos los lenguajes de programación se pueden representar como autómatas finitos. C, Paskal, Haskell, C++, todos tienen una estructura específica, gramática, que se puede representar mediante un gráfico simple. La mayoría de los gráficos son NFA o DFA. Pero NFA y DFA determinan el grupo de idiomas más simple posible: grupo de idiomas regulares [ jerarquía de Chomsky ]. Esto nos deja con una pregunta: ¿qué pasa con todos los demás tipos de lenguajes? Una de las respuestas es la máquina de Turing , pero una máquina de Turing es difícil de visualizar. Es por eso que en este artículo te hablaré de un tipo de autómata finito llamado L-grafo.

Para entender cómo funcionan los L-graphs necesitamos saber qué tipo de lenguajes determinan los L-graphs. En pocas palabras, los gráficos L representan tipos de lenguajes sensibles al contexto [y cualquier otro tipo que contenga el grupo sensible al contexto]. Si no sabe lo que significa «sensible al contexto», permítame mostrarle un ejemplo de un lenguaje que se puede representar mediante un gráfico en L y no mediante un tipo más sencillo de autómatas finitos.

Este lenguaje es $L = \{ a^nb^nc^n | n \geqslant 1 \}$ . El gráfico L correspondiente se ve así:

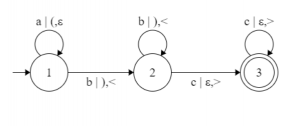
Como puede ver los corchetes después del símbolo ‘|’ controlar el número de símbolos que vienen después de los símbolos ‘a’. Esto nos lleva a las dos características que poseen todos los gráficos L: todos los gráficos L tienen hasta dos grupos de paréntesis independientes entre sí y de los símbolos de entrada, ambos grupos de paréntesis tienen que ser correctos [string de un lenguaje Dyck] para que la string de símbolos de entrada que aceptará el L-graph dado.

Puede ver que un L-graph es solo una versión de autómatas finitos con un par de grupos de corchetes adicionales. Para ayudarlo a comprender por qué los idiomas determinados por los gráficos L son sensibles al contexto, verifique qué strings debe aceptar el gráfico L que se muestra arriba.

$abc: \{\varepsilon, \varepsilon, \varepsilon\} \rightarrow \{a, (, \varepsilon} \rightarrow \{ab, (), <\} \rightarrow \{abc, (), <>\}\\* a^2b^2c^2: \{\varepsilon, \varepsilon, \varepsilon\} \rightarrow \{a, (, \varepsilon\} \rightarrow \{aa, ((, \varepsilon\} \rightarrow \{aab, ((), <\} \rightarrow \{aabb, (()), <<\} \rightarrow \{aabbc, (()), <<>\} \rightarrow \{aabbcc, (()), <<>>\}\\* a^5b^5c^5: \{\varepsilon, \varepsilon, \varepsilon\} \rightarrow \{a, (, \varepsilon\} \rightarrow \ldots \rightarrow \{aaaaa, (((((, \varepsilon\} \rightarrow \{aaaaab, (((((), <\} \rightarrow \ldots \rightarrow \{aaaaabbbbb, ((((())))), <<<<<\} \rightarrow \{aaaaabbbbbc, ((((())))), <<<<<>\} \rightarrow \ldots \rightarrow \{aaaaabbbbbccccc, ((((())))), <<<<<>>>>>\}$

Para concluir, me gustaría agregar otras tres definiciones que usaré en el futuro. Estas definiciones son muy importantes para la hipótesis [y su futura prueba o refutación]. Referir – Hipótesis (regularidad del lenguaje) y algoritmo (L-graph a NFA)

Llamaremos neutral a un camino en el L-graph, si ambas strings de paréntesis son correctas. Si un camino neutral T se puede representar así, T = $T_1T_2T_3$ , donde $T_1$ y $T_3$ son ciclos y $T_2$ es un camino neutral ( $T_1$ , $T_2$ o $T_3$ puede estar vacío), T se llama nido. También podemos decir que el tres ( $T_1$ , $T_2$ , $T_3$ ) es un nido o que $T_1$ y $T_3$ forman un nido en el camino T.

( $\omega$ , d)-núcleo en un L-grafo G, definido como Core(G, $\omega$ , d), es un conjunto de ( $\omega$ , d)-cánones. ( $\omega$ , d)-canon, donde $\omega$ y d son números enteros positivos, es un camino que contiene como máximo m, $m \leqslant \omega$ , ciclos neutros y como máximo k, k $k \leqslant d$ d, nidos que se pueden representar de esta manera: $T_1_1...T_1_kT_2_1T_3_1...T_3_k$ es parte del camino T, $T_i_l$ , i = 1 o 3, $1 \leqslant l \leqslant k$ , son ciclos, cada camino $T_1_jT_2_jT_3_j$ es un nido, donde $T_2_j$ = $T_1_(_j_-_1_)T_2_(_j_-_1_)T_3_(_j_-_1_)$ , $2 \leqslant j \leqslant k-1$ .

La última definición se trata de un gráfico L libre de contexto. Un L-grafo G se llama libre de contexto si G tiene solo un grupo de corchetes (todas las reglas en el L-grafo tienen solo un aspecto de estos dos: [‘símbolo’ | ‘corchete’, ?] o [‘símbolo’ | ? , ‘soporte’]).

[Definición de una lengua de Dyck. $\Sigma_($ y $\Sigma_)$ son alfabetos disjuntos. Existe una biyección (función que para cada elemento del 1er conjunto coincide con uno y solo un elemento del 2do conjunto) $\phi: \Sigma_( \rightarrow \Sigma_)$ . Entonces el lenguaje definido por la gramática $S \rightarrow \varepsilon | aSbS$ , $a \in \Sigma_(, b = \phi(a)$ lo llamaremos lenguaje de Dyck.]

Publicación traducida automáticamente

Artículo escrito por Fedor_S y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta