Gráficos por computadora: transformación de corte 3D

La transformación de corte es la misma que vemos en el espacio 2D, pero aquí tenemos que lidiar con los ejes x, y y z, mientras que en 2D solo tratamos con los ejes x e y. El corte es el proceso de inclinar un objeto en el espacio 3D, ya sea en la dirección x, y o en la dirección z. El cizallamiento cambia (o deforma) la forma del objeto. COMO estamos discutiendo el espacio 3D, el corte también se puede hacer en cualquiera de las tres direcciones de la siguiente manera. A continuación se presentan los tipos de transformación de corte.

Cortante en la dirección X.
Corte en dirección y
Corte en dirección z.

Corte en dirección X: aquí la coordenada de X permanece sin cambios mientras que la coordenada de Y y Z cambia. El cizallamiento se realiza a través de la array de Transformación de cizallamiento, que se representa de la siguiente manera.

$\hspace{6.08cm} \mathbf{S_x=\left [\begin{matrix}1&s_y&s_z&0\\0&1&0&0 \\0&0&1&0\\0&0&0&1\end{matrix}\right] }$

Considere un punto P[x, y, z] en el espacio 3D sobre el cual realizamos la transformación de corte en la dirección X y se convierte en P'[x, y, z].

$\mathbf{P'[x\hspace{0.2cm}y \hspace{0.2cm}z\hspace{0.2cm}1]= P[x_o\hspace{0.2cm}y_o\hspace{0.2cm}z_o\hspace {0.2cm}1].S_x}\\ \newline \hspace {6.08cm}\mathbf{P'[x, \hspace{0.2cm}y, \hspace{0.2cm}z]=[x_o, \hspace{0.2cm}y_n, \hspace{0.2cm}z_n]} \\$

$\textbf{The coordinate}\, \, \mathbf{P'[x_n, y_n, z_n]}\, \, \textbf{can also be calculated using below equations:} \newline \hspace{6.8cm}\mathbf{x_n = x_o \hspace{0.4cm}Remains\hspace{0.2cm}unchanged} \\ \hspace{6.8cm}\mathbf{y_n=y_o+s_y.x_o} \\ \hspace{6.8cm}\mathbf{z_n=z_o+s_z.x_0}\\$

Corte en la dirección Y: aquí la coordenada de Y permanece sin cambios mientras que las coordenadas de X y Z cambian. El cizallamiento se realiza a través de la array de Transformación de cizallamiento, que se representa de la siguiente manera.

$\mathbf{S_y= \left [\begin{matrix}1&0&0&0\\s_x&1&s_z&0 \\0&0&1&0\\0&0&0&1\end{matrix}\right] }$

Considere un punto P[x, y, z] en el espacio 3D sobre el cual realizamos la transformación de corte en la dirección Y y se convierte en P'[x, y, z].

$\mathbf{P'[x\hspace{0.2cm}y \hspace{0.2cm}z\hspace{0.2cm}1]=P[x_o\hspace {0.2cm}y_o\hspace{0.2cm}z_o\hspace{0.2cm}1].S_y} \\ \newline \hspace{6.08cm}\mathbf{P'[x, \hspace{0.2cm}y, \hspace{0.2cm}z]=[x_n, \hspace{0.2cm}y_o, \hspace{0.2cm}z_n]} \\ \newline$

$\textbf{The coordinate}\, \, \mathbf{P'[x_n, y_n, z_n]}\, \, \textbf{can also be calculated using below equations:} \newline \hspace{6.8cm}\mathbf{x_n = x_o+s_x.y_o } \\ \hspace{6.8cm}\mathbf{y_n=y_o \hspace{0.4cm}Remains \hspace{0.2cm}unchanged}\\ \hspace{6.8cm} \mathbf{z_n=z_o+s_z.y_o }\\$

Corte en dirección Z: aquí la coordenada de Z permanece sin cambios mientras que las coordenadas de X e Y cambian. El corte se realiza a través de la array de transformación de corte, que se representa de la siguiente manera para el corte en la dirección Z.

$\mathbf{S_z =\left [\begin{matrix}1&0&0&0 \\0&1&0&0\\s_x&s_y&1&0 \\0&0&0&1\end{matrix}\right] }$

Considere un punto P[x, y, z] en el espacio 3D sobre el cual realizamos la transformación de corte en la dirección Z y se convierte en P'[x, y, z].

$\mathbf{P'[x\hspace{0.2cm} y\hspace{0.2cm}z\hspace{0.2cm}1]=P[x_o \hspace{0.2cm}y_o\hspace{0.2cm}z_o\hspace {0.2cm}1].S_z}\\ \newline \hspace{6.08cm} \mathbf{P'[x, \hspace{0.2cm}y, \hspace{0.2cm}z]=[x_n, \hspace{0.2cm}y_n, \hspace{0.2cm}z_o]}\\$

$\textbf{The coordinate}\, \, \mathbf{P'[x_n, y_n, z_n]}\, \, \textbf{can also be calculated using below equations:} \newline \hspace{6.8cm}\mathbf{x_n = x_o+s_x.z_o } \\ \hspace{6.8cm}\mathbf{y_n=y_o+s_y.z_o} \\ \hspace{6.8cm}\mathbf{z_n=z_o \hspace{0.4cm}Remains \hspace{0.2cm}unchanged}\\$

Nota: Aquí, x _n , y _n , z _n muestran = valores nuevos y x _o , y _o , z _o muestran = valores antiguos.

Realice la Transformación de corte en el cuboide dado (OABCDEFG) a lo largo de la dirección Z si un parámetro de corte es el siguiente S _x = 2, S _y = 3.

La array de transformación de corte para la dirección z es la siguiente.

$\mathbf{S_z=\left [\begin{matrix}1&0&0&0\\0&1&0&0\\s_x&s_y&1&0 \\0&0&0&1\end{matrix}\right]}$

Y el cuboide dado es el siguiente:

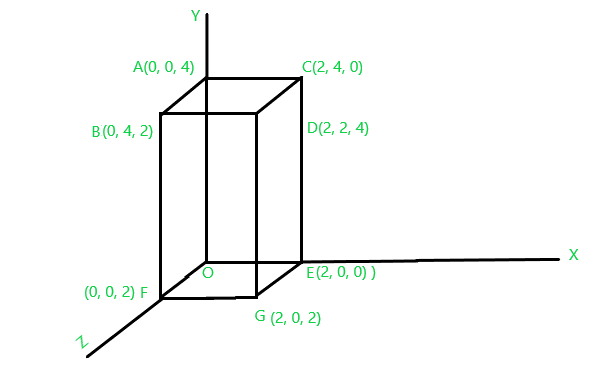
Figura 1

Ahora, aplicaremos la condición de transformación de corte sobre todas las coordenadas y calcularemos las nuevas coordenadas correspondientes:

El punto O[0, 0, 0] se convierte en O’ después de realizar la transformación de reflexión:

$\mathbf {O'[x\hspace{0.2cm}y\hspace {0.2cm}z\hspace{0.2cm}1]= [0\hspace{0.2cm}0\hspace{0.2cm}0 \hspace{0.2cm}1]\left [\begin{matrix}1&0&0&0 \\0&1&0&0\\2&3&1&0\\0&0&0&1 \end{matrix}\right]} \\ \newline \hspace{7.09cm}\mathbf{= [\hspace{0.2cm}0\hspace{0.2cm}0\hspace {0.2cm}0\hspace{0.2cm}1]}\\ \newline \hspace{4.37cm}\mathbf {O'[x\hspace{0.2cm}y\hspace {0.2cm}z\hspace{0.2cm}1]= [\hspace{0.2cm}0\hspace{0.2cm}0 \hspace{0.2cm}0\hspace{0.2cm}1]}$

El punto A'[0, 0, 4] se convierte en A’ después de realizar la transformación de reflexión:

$\mathbf{A'[x \hspace {0.2cm}y\hspace{0.2cm}z \hspace{0.2cm}1] = [0\hspace{0.2cm}0\hspace{0.2cm}4 \hspace {0.2cm}1]\left [\begin{matrix} 1&0&0&0 \\0&1&0&0\\2&3&1&0\\0&0&0&1\end {matrix}\right]} \\ \newline \hspace {7.09cm}\mathbf{= [8\hspace{0.2cm}12\hspace {0.2cm}4\hspace{0.2cm}1]} \\ \newline \hspace {4.37cm}\mathbf{A'[x\hspace{0.2cm}, y\hspace{0.2cm}, z]= [8\hspace{0.2cm}12 \hspace{0.2cm}4]}$

El punto B'[0, 0, 4] se convierte en B’ después de realizar la transformación de reflexión:

$\mathbf{B' [x\hspace{0.2cm}y\hspace {0.2cm}z\hspace{0.2cm}1]= [0\hspace{0.2cm}4\hspace{0.2cm}2\hspace{0.2cm}1] \left [\begin{matrix}1&0&0&0\\0&1&0&0 \\2&3&1&0\\0&0&0&1\end{matrix}\right]} \\ \newline \hspace{7.09cm}\mathbf{= [8\hspace{0.2cm}10\hspace{0.2cm}2\hspace{0.2cm}1]} \\ \newline \hspace{4.37cm}\mathbf{B'[x\hspace{0.2cm}, y\hspace{0.2cm}, z]=[8\hspace{0.2cm}10\hspace{0.2cm}2]}$

El punto C'[2, 4, 0] se convierte en C’ después de realizar la transformación de reflexión:

$\mathbf{C'[x\hspace{0.2cm}y \hspace{0.2cm}z\hspace{0.2cm}1]= [2\hspace{0.2cm}4\hspace{0.2cm}0 \hspace{0.2cm}1]\left [\begin{matrix}1&0&0&0 \\0&1&0&0\\2&3&1&0 \\0&0&0&1\end{matrix}\right]} \\ \newline \hspace {7.09cm}\mathbf{= [2\hspace{0.2cm}4\hspace {0.2cm}0\hspace{0.2cm}1]}\\ \newline \mathbf{C'[x\hspace{0.2cm}, y\hspace{0.2cm}, z]= [2\hspace{0.2cm}4\hspace {0.2cm}0]}$

El punto D'[2, 2, 4] se convierte en D’ después de realizar la transformación de reflexión:

$\mathbf{D'[x\hspace{0.2cm}y \hspace{0.2cm}z\hspace{0.2cm}1]= [2\hspace{0.2cm}2\hspace{0.2cm}4\hspace {0.2cm}1]\left [\begin{matrix}1&0&0&0 \\0&1&0&0\\2&3&1&0\\0&0&0&1\end{matrix}\right] } \\ \newline \hspace{7.09cm}\mathbf{= [10\hspace{0.2cm}14\hspace{0.2cm}4\hspace{0.2cm}1] }\\ \newline \hspace{4.37cm}\mathbf{D'[x\hspace{0.2cm} , y\hspace{0.2cm}, z]=[10\hspace{0.2cm}14 \hspace{0.2cm}4]}$

El punto E'[2, 0, 0] se convierte en E’ después de realizar la transformación de reflexión:

$\mathbf{E' [x\hspace{0.2cm}y\hspace {0.2cm}z\hspace{0.2cm}1]= [2\hspace{0.2cm}0\hspace {0.2cm}0\hspace{0.2cm}1] \left [\begin{matrix}1&0&0&0 \\0&1&0&0\\2&3&1&0 \\0&0&0&1\end{matrix}\right]} \\ \newline \hspace{7.09cm}\mathbf{= [2\hspace{0.2cm}0\hspace{0.2cm}0\hspace{0.2cm}1]} \\ \newline \hspace{4.37cm}\mathbf{E'[x\hspace{0.2cm}, y\hspace{0.2cm}, z]=[2\hspace{0.2cm}0\hspace{0.2cm}0]}$

El punto F'[ 0, 0, 2] se convierte en F’ después de realizar la transformación de reflexión:

$\mathbf {F'[x\hspace{0.2cm}y\hspace{0.2cm}z \hspace{0.2cm}1]=[0\hspace{0.2cm}0\hspace {0.2cm}2\hspace{0.2cm}1]\left [\begin{matrix}1&0&0&0\\0&1&0&0\\2&3&1&0 \\0&0&0&1\end{matrix}\right]} \\ \newline \hspace{7.09cm}\mathbf{= [4\hspace{0.2cm}6\hspace{0.2cm}2\hspace{0.2cm}1]} \\ \newline \hspace{4.37cm}\mathbf{F'[x\hspace{0.2cm}, y\hspace{0.2cm}, z]=[4\hspace{0.2cm}6\hspace{0.2cm}2]}$

El punto G'[2, 0, 2] se convierte en G’ después de realizar la transformación de reflexión:

$\mathbf{G'[x\hspace{0.2cm}y \hspace{0.2cm}z\hspace{0.2cm}1]=[2\hspace{0.2cm}0 \hspace{0.2cm}2\hspace{0.2cm}1]\left [\begin{matrix}1&0&0&0\\0&1&0&0\\2&3&1&0 \\0&0&0&1\end{matrix}\right]} \\ \newline \hspace{7.09cm}\mathbf{= [6\hspace{0.2cm}6\hspace{0.2cm}2\hspace{0.2cm}1]} \\ \newline \hspace{4.37cm}\mathbf {G'[x\hspace{0.2cm}, y\hspace{0.2cm}, z]= [6\hspace{0.2cm}6\hspace{0.2cm}2]}$

Finalmente, después de realizar la transformación de corte en el cuboide dado, su figura 1 se verá como se muestra a continuación:

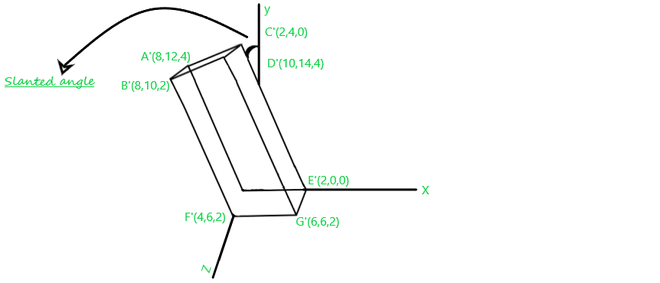
Figura 2

Publicación traducida automáticamente

Artículo escrito por madhav_mohan y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta