gramática ambigua

• Número de árboles de derivación
• Número de cuerdas

 
Según el número de árboles de derivación, los CFG se subdividen en 2 tipos:

• gramáticas ambiguas
• Gramáticas inequívocas

 
Gramática ambigua:
 
se dice que un CFG es ambiguo si existe más de un árbol de derivación para la string de entrada dada, es decir, más de un árbol de derivación más a la izquierda ( LMDT ) o más de un árbol de derivación más a la derecha ( RMDT ) . Definición: G = (V,T,P,S) es un CFG que se dice que es ambiguo si y solo si existe una string en T* que tiene más de un árbol de análisis. donde V es un conjunto finito de variables. T es un conjunto finito de terminales. P es un conjunto finito de producciones de la forma A -> α, donde A es una variable y α ∈ (V ∪ T)* S es una variable designada llamada símbolo de inicio.  
 

 
Por ejemplo:
 
1. Consideremos esta gramática: E -> E+E|id

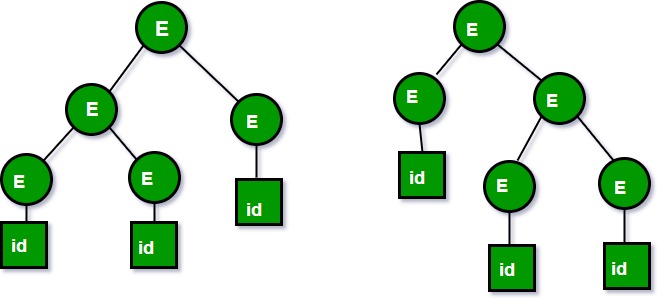
Podemos crear 2 árboles de análisis a partir de esta gramática para obtener una string id+id+id   :

Los siguientes son los 2 árboles de análisis generados por la derivación más a la izquierda:

Los dos árboles de análisis anteriores se derivan de las mismas reglas gramaticales, pero ambos árboles de análisis son diferentes. Por lo tanto, la gramática es ambigua.  
 
2. Consideremos ahora la siguiente gramática:
 

Set of alphabets ∑ = {0,…,9, +, *, (, )}

E -> I        
E -> E + E
E -> E * E
E -> (E)
I -> ε | 0 | 1 | … | 9
 

De la gramática anterior, String 3*2+5 se puede derivar de 2 maneras:
 

I) First leftmost derivation                   II) Second leftmost derivation
        E=>E*E                          E=>E+E
         =>I*E                           =>E*E+E
         =>3*E+E                                       =>I*E+E
         =>3*I+E                           =>3*E+E
         =>3*2+E                           =>3*I+E
         =>3*2+I                           =>3*2+I
         =>3*2+5                           =>3*2+5

 
Los siguientes son algunos ejemplos de gramáticas ambiguas:
 

• S-> aS |Sa| Є
• E-> E +E | E*E| identificación
• A -> AA | (A) | a
• S -> SS|AB, A -> Aa|a, B -> Bb|b

Mientras que las siguientes gramáticas son inequívocas:
 

• S -> (L) | a, L -> LS | S
• S -> AA , A -> aA , A -> b

Lenguaje inherentemente ambiguo:  
 
Sea L un lenguaje libre de contexto (CFL). Si toda gramática libre de contexto G con lenguaje L = L(G) es ambigua, entonces se dice que L es un lenguaje inherentemente ambiguo. La ambigüedad es una propiedad de la gramática, no de los idiomas. Es poco probable que la gramática ambigua sea útil para un lenguaje de programación, porque dos estructuras de árboles de análisis (o más) para la misma string (programa) implican dos significados diferentes (programas ejecutables) para el programa.

Un lenguaje inherentemente ambiguo sería absolutamente inadecuado como lenguaje de programación, porque no tendríamos ninguna forma de fijar una estructura única para todos sus programas.

Por ejemplo,

L = {anbncm} ∪ {anbmcm} 

 
Nota: la ambigüedad de la gramática es indecidible, es decir, no existe un algoritmo particular para eliminar la ambigüedad de la gramática, pero podemos eliminar la ambigüedad al: Eliminar la ambigüedad de  
 
la gramática , es decir, reescribir la gramática de modo que solo haya una derivación o árbol de análisis posible para una string de la lengua que representa la gramática.  
 

Este artículo ha sido compilado por Saikiran Goud Burra .
 
Escriba comentarios si encuentra algo incorrecto o si desea compartir más información sobre el tema tratado anteriormente.