GRE Álgebra | Resolver ecuaciones cuadráticas

En álgebra, una ecuación cuadrática se puede escribir en la forma:

ax2 + bx + c = 0 

donde x es la variable y a, b, c son los números reales y a≠0. Si a=0 entonces será una ecuación lineal no cuadrática porque no hay término de segundo orden.

Si la ecuación cuadrática tiene solución, entonces se puede encontrar usando la fórmula cuadrática .

• Ejemplo-1: Resuelva la ecuación cuadrática para x,

  x2 + 10x -24 = 0 

  Solución: En la ecuación cuadrática tenemos,

  a=1, b=10 and c=-24 

  Por lo tanto, la fórmula cuadrática da

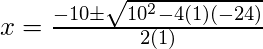
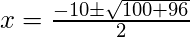
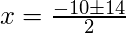
  Por lo tanto, dos soluciones para las ecuaciones anteriores son:

  x = 4/2 = 2,
  And
  x = -24/2 = -12 

• Ejemplo-2: Resolver la ecuación cuadrática usando factorización,

  x2 + 2x - 15 = 0

  Solución: Ecuación dada,

  x2 + 2x - 15 = 0 

  Se puede factorizar como,

  x2 -3x + 5x - 15 = 0
  x(x - 3) + 5(x - 3) = 0
  (x - 3)(x + 5) = 0 

  Por lo tanto, dos soluciones para x son:

  x = 3 and x = -5