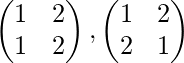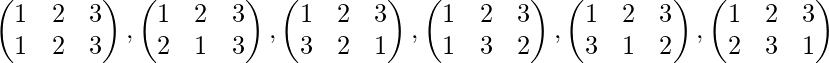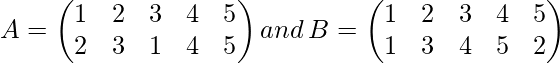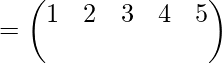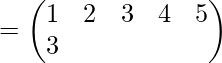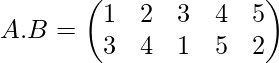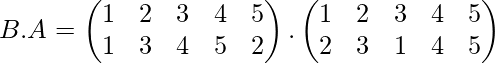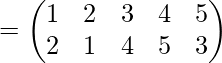Grupos de permutación y multiplicación de permutación

Sea G un conjunto no vacío, entonces una correspondencia de uno a sí mismo que se muestra a continuación se llama permutación.

El número de elementos en el conjunto finito G se llama grado de permutación.
Si G tiene n elementos, entonces P _n se llama un conjunto de todas las permutaciones de grado n.
P _n también se llama grupo simétrico de grado n.
P _n también se denota por S _n .
El número de elementos en P _n o S _ⁿ es $¡norte!$

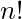
Ejemplos:

Caso 1: Sea G={ 1 } elemento, entonces las permutaciones son S _n o P _n = $\begin{pmatrix} 1 \\ 1 \end{pmatrix}$

Caso 2: Sea G= { 1, 2 } elementos, entonces las permutaciones son $\begin{pmatrix} 1 y 2\\ 1 y 2 \end{pmatrix} , \begin{pmatrix} 1 y 2\\ 2 y 1 \end{pmatrix}$

Caso 3: Sea G={ 1, 2, 3 } elementos, entonces la permutación es 3!=6. Estos son,

$\begin{pmatrix} 1 y 2 y 3\\ 1 y 2 y 3 \end{pmatrix} , \begin{pmatrix} 1 y 2 y 3\\ 2 y 1 y 3 \end{pmatrix} , \begin{pmatrix} 1 & 2 & 3\\ 3 & 2 & 1 \end{pmatrix} , \begin{pmatrix} 1 & 2 & 3\\ 1 & 3 & 2 \end{pmatrix} , \begin{pmatrix} 1 & 2 & 3 \\ 3 y 1 y 2 \end{pmatrix} , \begin{pmatrix} 1 y 2 y 3\\ 2 y 3 y 1 \end{pmatrix}$

Lectura del símbolo de permutación

Supongamos que una permutación es 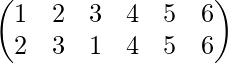$\begin{pmatrix} 1 & 2 & 3 &4 &5&6\\ 2&3&1&4&5&6 \end{pmatrix}$

Primero, vemos que en un paréntesis pequeño hay dos filas escritas, estas dos filas tienen números. El número más pequeño es 1 y el número más grande es 6.
Comenzando desde el lado izquierdo de la primera fila, leemos como una imagen de 1 es 2, una imagen de 1 es 2, una imagen de 2 es 3, una imagen de 3 es 1, una imagen de 4 es 4 (Imagen propia = idéntico=identidad) , una imagen de 5 es 6 y una imagen de 6 es 5.
Lo anterior también se puede leer como: Comenzando desde el lado izquierdo de la primera fila, 1 va a 2, 2 va a 3, 3 va a, 4 va a 4, 5 va a 6 y 6 va a 5.

Un ciclo de longitud 2 se llama permutación.

Ejemplo:

1) $\begin{pmatrix} 4 y 5\\ \end{pmatrix}$

La longitud es 2, por lo que es una transposición.

2) $\begin{pmatrix} 1 & 2 & 3\\ \end{pmatrix}$

La longitud es tres, por lo que no es una transposición.

Multiplicación de permutación

problema: si $A= \begin{pmatrix} 1 & 2 & 3&4&5\\ 2&3&1&4&5 \end{pmatrix} and \,B= \begin{pmatrix} 1 & 2 & 3 &4&5\\ 1&3&4&5&2 \end{pmatrix}$

Encuentra el producto de la permutación AB y BA

Solución: $A= \begin{pmatrix} 1 & 2 & 3&4&5\\ 2&3&1&4&5 \end{pmatrix} and \,B= \begin{pmatrix} 1 & 2 & 3 &4&5\\ 1&3&4&5&2 \end{pmatrix}$

$A.B= \begin{pmatrix} 1 & 2 & 3&4&5\\ 2&3&1&4&5 \end{pmatrix} . \begin{pmatrix} 1 & 2 & 3 &4&5\\ 1&3&4&5&2 \end{pmatrix}$

$= \begin{pmatrix} 1 & 2 & 3&4&5\\ &&&& \end{pmatrix}$

Aquí podemos ver que en el primer paréntesis 1 va a 2, es decir, la imagen de 1 es 2, y en la segunda fila 2 va a 3, es decir, la imagen de 2 es 3.

Por lo tanto, escribiremos 3 debajo de 1 en el paréntesis que se muestra a continuación,

$= \begin{pmatrix} 1 & 2 & 3&4&5\\ 3&&&& \end{pmatrix}$

Realice el paso anterior con todos los elementos de la primera fila, la respuesta será

$A.B= \begin{pmatrix} 1 & 2 & 3&4&5\\ 3&4&1&5&2 \end{pmatrix}$

Similarmente,

$B.A= \begin{pmatrix} 1 & 2 & 3&4&5\\ 1&3&4&5&2 \end{pmatrix} . \begin{pmatrix} 1 & 2 & 3 &4&5\\ 2&3&1&4&5 \end{pmatrix}$

$= \begin{pmatrix} 1 & 2 & 3&4&5\\ 2&1&4&5&3 \end{pmatrix}$

Publicación traducida automáticamente

Artículo escrito por portalpirate y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA

Deja una respuesta Cancelar la respuesta