Matrix es el conjunto de números dispuestos en filas y columnas para formar una array rectangular. Aquí, esos números se llaman las entradas o elementos de esa array. Una array rectangular de (m*n) números en forma de ‘m’ líneas horizontales (filas) y ‘n’ líneas verticales (llamadas columnas), se denomina array de orden m por n, que se escribe como m × n array.
Nota: Si m=n, es decir, Número de Filas = Número de Columnas en una Array ‘A’, entonces se dice que ‘A’ es una Array Cuadrada de orden ‘n’.
La inversa de una array cuadrada:
Si ‘A’ es una array cuadrada no singular (|A| ≠ 0) de orden ‘n’, entonces existe una array A -1 de nxn , que se denomina array inversa de ‘A’, que satisface la siguiente propiedad :
AA-1 = A-1A = In, where In is the Identity matrix of order n
Podemos encontrar el inverso de una array cuadrada usando varios métodos como:
- Método Cayley-Hamilton
- Eliminación gaussiana
- Método de Newton
- Método de descomposición de Eigen
Teorema de Cayley-Hamilton:
En el Dominio del Álgebra Lineal, según el teorema de Cayley-Hamilton, toda array cuadrada ‘A’ de orden ‘n’ satisface su propia ecuación característica, la cual viene dada por:
|A-λIn| = 0 Here 'In' is the Identity Matrix of Order 'n' (same as that of A's Order) and 'λ' is some Real Constant.
Expandiendo la ecuación característica anterior de ‘A’, obtenemos:
λn + C1λn-1 + C2λn-2 + . . . + CnIn = 0, where C1, C2, . . . , Cn are Real Constants.
De acuerdo con el teorema de Cayley-Hamilton, la ecuación característica anterior de ‘A’ se satisface por sí misma, por lo que tenemos:
An + C1An-1 + C2An-2+ . . . + CnIn = 0 , where C1, C2, . . . , Cn are Real Constants.
Pasos para encontrar el inverso de una array cuadrada usando el teorema de Cayley Hamilton:
Paso 1: Para una array cuadrada no singular dada ‘A’ de orden ‘n’, encuentre su ecuación característica |A-λI n | = 0.
Expanda el Determinante de modo que se reduzca en el siguiente formato:
λn + C1λn-1 + C2λn-2 + . . . + CnIn = 0, where C1, C2, . . . , Cn are Real Constants.
Paso 2: Según el teorema de Cayley-Hamilton, la ecuación característica anterior de ‘A’ se satisface por sí misma, por lo tanto:
An + C1An-1 + C2An-2 + . . . + CnIn = 0
Paso 3: Multiplicar por A -1 en ambos lados de la ecuación anterior la reduce a:
An-1 + C1An-2 + C2An-3 + . . . Cn-1In + CnA-1 = 0
Paso 4: Encuentra A -1 simplificando y reordenando los términos de la ecuación anterior, entonces A -1 es:
A-1 = (-1/Cn)[ An-1 + C1An-2 + C2An-3 + . . . Cn-1In ]
Las funciones de MATLAB utilizadas en el siguiente código son:
- disp(“txt”): este método muestra el mensaje-‘txt’ al usuario.
- entrada («txt»): este método muestra el mensaje-‘txt’ y espera a que el usuario ingrese un valor y presione la tecla Retorno.
- poly(A): Este método devuelve los n+1 coeficientes del polinomio Característica de la array ‘A’ de orden ‘n’.
- length(X): Este método devuelve el número de elementos del vector ‘X’.
- round(x): este método redondea ‘x’ a su entero más cercano.
Ejemplo:
Matlab
% MATLAB Implementation to find Inverse
% of a Square Matrix using Cayley Hamilton theorem:
clear all
clc
disp("Finding Inverse of a Square Matrix using
Cayley Hamilton theorem in MATLAB | GeeksforGeeks")
A=input('Enter the Matrix A: ');
% To find Coefficients of Characteristic Equation of Matrix 'A'
cf=poly(A);
% To find the Number of Coefficients in
% the Characteristic Equation of Matrix 'A'
n=length(cf);
% To find the Inverse of A
inverse = cf(1)*A^(n-2);
for i=2:n-1
inverse=inverse+cf(i)*A^(n-i-1);
end
% Checking whether |A|=0 or not
if round(cf(n))==0
disp('Inverse of A does not exist as it is a singular matrix..')
else
inverse=inverse/(-cf(n));
disp('Inverse of A: ')
disp(inverse)
end
Producción:
Array de entrada:
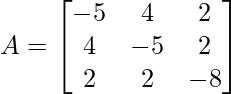

Array de entrada:
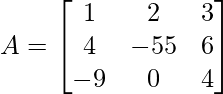

Array de entrada:
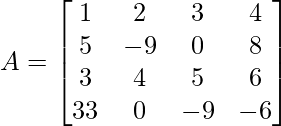

Publicación traducida automáticamente
Artículo escrito por kothavvsaakash y traducido por Barcelona Geeks. The original can be accessed here. Licence: CCBY-SA